题目内容
设函数
 .
.
(1) 试问函数f(x)能否在x=  时取得极值?说明理由;
时取得极值?说明理由;
(2) 若a=  ,当x∈[
,当x∈[ ,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
(1)f(x)在x=-1处无极值. (2) 或c=
或c=
解析试题分析:解:(1) 由题意f′(x)=x2-2ax-a,
假设在x= -1时f(x)取得极值,则有f′(-1)=1+2a-a=0,∴a=-1,
而此时,f′(x)=x2+2x+1=(x+1)2≥0,函数f(x)在R上为增函数,无极值.
这与f(x)在x=-1有极值矛盾,所以f(x)在x=-1处无极值.
(2) 设f(x)=g(x),则有 x3-x2-3x-c=0,∴c=
x3-x2-3x-c=0,∴c= x3-x2-3x,
x3-x2-3x,
设F(x)=  x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0,解得x1=-1或x=3.
x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0,解得x1=-1或x=3.
列表如下:
由此可知:F(x)在(-3,-1)、(3,4)上是增函数,在(-1,3)上是减函数.x -3 (-3,-1) -1 (-1,3) 3 (3,4) 4 F′(x) + 0 - 0 + F(x) -9 增 
减 -9 增  -
-
当x=-1时,F(x)取得极大值 ;当x=3时,F(x)取得极小值
;当x=3时,F(x)取得极小值
F(-3)=F(3)=-9,而 .
.
如果函数f(x)与g(x)的图像有两个公共点,则函数F(x)与G(x)有两个公共点,
所以 或c=
或c=
考点:导数的运用
点评:主要是考查了导数在研究函数单调性以及函数极值中的运用,属于基础题。

练习册系列答案
相关题目

 .
. 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围; 上的最小值.
上的最小值. 中,
中, ,点
,点 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。 的通项公式;
的通项公式;  , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出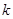 值;若不存在,说明理由;
值;若不存在,说明理由; ,不等式
,不等式 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。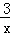 )元.
)元. )元;
)元;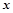 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数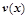 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)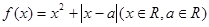 .
. 时,求
时,求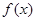 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的二次项系数为
的二次项系数为 ,满足不等式
,满足不等式 的解集为(1,3),且方程
的解集为(1,3),且方程 有两个相等的实根,求
有两个相等的实根,求 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数