题目内容
将边长为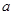 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
V(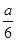 )=
)=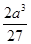 , 即为容积的最大值,此时小正方形的边长为
, 即为容积的最大值,此时小正方形的边长为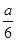 .
.
解析试题分析:设小正方形的边长为x,则盒底的边长为a-2x,
∴方盒的体积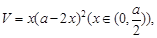 4分
4分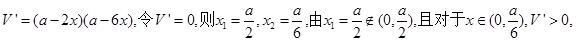
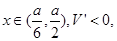 10分
10分
∴函数V在点x=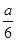 处取得极大值,由于问题的最大值存在,
处取得极大值,由于问题的最大值存在,
∴V(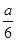 )=
)=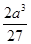 , 即为容积的最大值,此时小正方形的边长为
, 即为容积的最大值,此时小正方形的边长为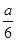 . 12分
. 12分
考点:函数模型,应用导数研究函数的最值。
点评:中档题,作为应用问题,往往涉及确定函数的最值。求最值的方法有,不等式法、导数法等。实际问题中,当驻点个数只有一个时,其既是极值点也是最值点。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
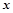 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数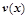 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) %,则销售量将减少
%,则销售量将减少 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过 %,
%, 其中
其中 为正常数
为正常数

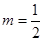 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 在
在 处取得极小值.
处取得极小值. 的值;
的值; 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线 不可能在直线
不可能在直线 ,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.  )
) ,及函数
,及函数 。
。 的不等式
的不等式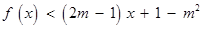 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

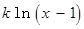 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且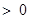 ,求证:
,求证:
 。
。 (
(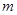 为常数,
为常数, ),且数列
),且数列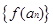 是首项为
是首项为 ,公差为
,公差为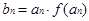 ,当
,当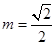 时,求数列
时,求数列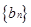 的前
的前 项和
项和 ;
; 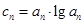 ,如果
,如果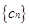 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求