题目内容
若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
(1) f(x)=x2-x+1.(2) (-∞,-1).
解析试题分析:(1)由f(0)=1得,c=1. 1分
∴f(x)=ax2+bx+1.又f(x+1)-f(x)=2x,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,∴ ∴
∴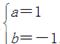 5分
5分
因此,f(x)=x2-x+1.
(2)f(x)>2x+m等价于x2-x+1>2x+m, 6分
即x2-3x+1-m>0,要使此不等式在[-1,1]上恒成立,
只需使函数g(x)=x2-3x+1-m在[-1,1]上的最小值大于0即可. 8分
∵g(x)=x2-3x+1-m在[-1,1]上单调递减,
∴g(x)min=g(1)=-m-1, 10分
由-m-1>0得,m<-1.
因此满足条件的实数m的取值范围是(-∞,-1). 12分
考点:本题考查了一元二次函数及其恒成立问题
点评:对于二次函数f(x)=ax2+bx+c=0(a≠0)在实数集R上恒成立问题可利用判别式直接求解,即:f(x)>0恒成立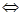

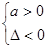 ;f(x)<0恒成立
;f(x)<0恒成立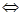

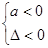 ,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解
,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 中,
中, ,点
,点 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。 的通项公式;
的通项公式;  , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出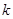 值;若不存在,说明理由;
值;若不存在,说明理由; ,不等式
,不等式 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。 的二次项系数为
的二次项系数为 ,满足不等式
,满足不等式 的解集为(1,3),且方程
的解集为(1,3),且方程 有两个相等的实根,求
有两个相等的实根,求 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 %,则销售量将减少
%,则销售量将减少 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过 %,
%, 其中
其中 为正常数
为正常数

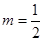 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?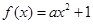 (
( ),
), .
. 与
与 处具有公共切线,求
处具有公共切线,求 的值;
的值; 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值. (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). 的解析式及其定义域;
的解析式及其定义域;