题目内容
 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.(Ⅰ)求二面角M-AC-B大小的正切值;
(Ⅱ)求三棱锥P-MAC的体积.
(1)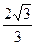 (2)
(2)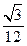
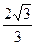 (2)
(2)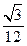
方法一:(Ⅰ)取BC的中点N,连结MN.
由已知,PM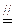 CN,则MN
CN,则MN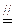 PC,所以MN⊥平面ABC.
PC,所以MN⊥平面ABC.
过点N作NH⊥AC,交AC的延长线于H,连结MH,
由三垂线定理知,AC⊥MH.
所以∠MHN为二面角M-AC-B的平面角.
连结AN,在△ACN中,由余弦定理,得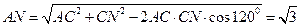 .
.
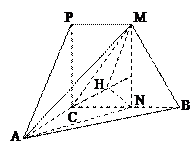 由已知∠AMN=60°,在Rt△ANM中,
由已知∠AMN=60°,在Rt△ANM中,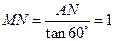 .
.
在Rt△CHN中,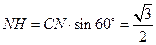 .
.
在Rt△MNH中,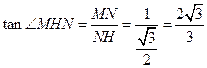 .
.
故二面角M-AC-B的正切值是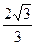 .
.
(Ⅱ)因为四边形PCNM为正方形,MN⊥平面ABC,则
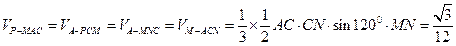 .
.
 方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,
方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,
按如图所示建立空间直角坐标系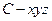 .
.
设点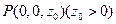 ,由已知可得,点
,由已知可得,点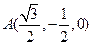 ,
,
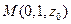 ,则
,则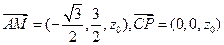 .
.
因为直线AM与直线PC所成的角为60°,则
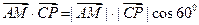 ,即
,即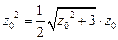 .
.
解得z0=1,从而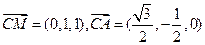 .
.
设平面MAC的一个法向量为n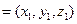 ,则
,则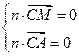 ,即
,即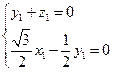 .
.
取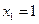 ,则n
,则n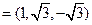 .
.
又m=(0,0,1)为平面ABC的一个法向量,设向量m与n的夹角为θ,则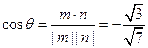 .
.
从而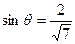 ,
,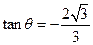 .
.
显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的正切值是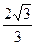 .
.
(Ⅱ)因为a=(1,0,0)为平面PCM的一个法向量, ,则
,则
点A到平面PCM的距离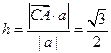 .
.
又PC=PM=1,则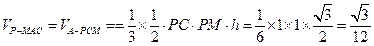 .
.
由已知,PM
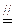 CN,则MN
CN,则MN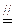 PC,所以MN⊥平面ABC.
PC,所以MN⊥平面ABC. 过点N作NH⊥AC,交AC的延长线于H,连结MH,
由三垂线定理知,AC⊥MH.
所以∠MHN为二面角M-AC-B的平面角.
连结AN,在△ACN中,由余弦定理,得
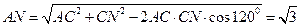 .
. 由已知∠AMN=60°,在Rt△ANM中,
由已知∠AMN=60°,在Rt△ANM中,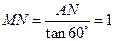 .
. 在Rt△CHN中,
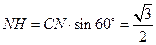 .
. 在Rt△MNH中,
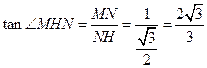 .
. 故二面角M-AC-B的正切值是
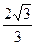 .
. (Ⅱ)因为四边形PCNM为正方形,MN⊥平面ABC,则
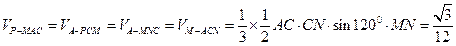 .
.  方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,
方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,按如图所示建立空间直角坐标系
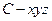 .
. 设点
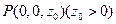 ,由已知可得,点
,由已知可得,点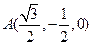 ,
,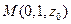 ,则
,则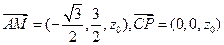 .
.因为直线AM与直线PC所成的角为60°,则
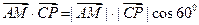 ,即
,即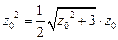 .
.解得z0=1,从而
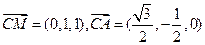 .
. 设平面MAC的一个法向量为n
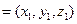 ,则
,则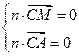 ,即
,即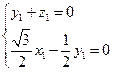 .
.取
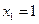 ,则n
,则n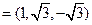 .
. 又m=(0,0,1)为平面ABC的一个法向量,设向量m与n的夹角为θ,则
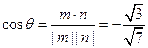 .
.从而
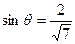 ,
,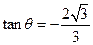 .
. 显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的正切值是
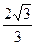 .
. (Ⅱ)因为a=(1,0,0)为平面PCM的一个法向量,
 ,则
,则点A到平面PCM的距离
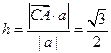 .
. 又PC=PM=1,则
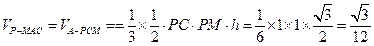 .
. 
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
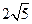 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交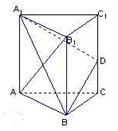
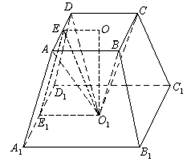
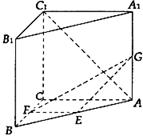
 中,
中,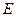 为
为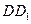 上的点、
上的点、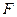 为
为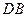 的中点.
的中点.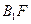 与平面
与平面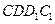 所成角的正弦值;
所成角的正弦值;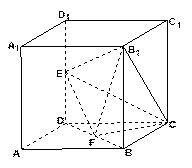 (Ⅱ)若直线
(Ⅱ)若直线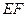 //平面
//平面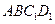 ,试确定点
,试确定点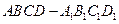 的棱
的棱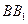 和
和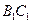 的中点,求:
的中点,求: 所成的角;
所成的角;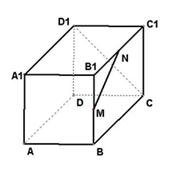
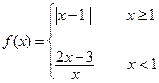 ,解不等式
,解不等式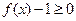 .
.