题目内容
在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.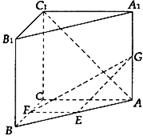
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小.

(Ⅰ)中点(Ⅱ)

解法一:(Ⅰ)以C为原点,分别以CB、CA、CC1为x轴、y轴、z轴建立空间直角坐标系,则F(1,0,0),E(1,1,0),A(0,2,0),C1(0,0,2),
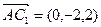
设G(0,2,h),则
∴-1×0+1×(-2)+2h="0. " ∴h=1,即G是AA1的中点.
(Ⅱ)设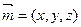 是平面EFG的法向量,则
是平面EFG的法向量,则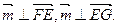
所以 平面EFG的一个法向量m=(1,0,1)
平面EFG的一个法向量m=(1,0,1)
∵
∴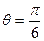 ,即AC1与平面EFG所成角
,即AC1与平面EFG所成角 为
为
解法二:(Ⅰ)取AC的中点D,连结DE、DG,则ED//BC
∵BC⊥AC,∴ED⊥AC.又CC1⊥平面ABC,而ED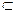 平面ABC,∴CC1⊥ED.
平面ABC,∴CC1⊥ED.
∵CC1∩AC=C,∴ED⊥平面A1ACC1.
又∵AC1⊥EG,∴AC1⊥DG.
连结A1C,∵AC1⊥A1C,∴A1C//DG.
∵D是AC的中点,∴G是AA1的中点.
(Ⅱ)取CC1的中点M,连结GM、FM,则EF//GM,
∴E、F、M、G共面.作C1H⊥FM,交FM的延长线于H,∵AC⊥平面BB1C1C,
C1H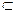 平面BB1C1C,∴AC⊥G1H,又AC//GM,∴GM⊥C1H. ∵GM∩FM=M,
平面BB1C1C,∴AC⊥G1H,又AC//GM,∴GM⊥C1H. ∵GM∩FM=M,
∴C1H⊥平面EFG,设AC1与MG相交于N点,所以∠C1NH为直线AC1与平面EFG所成角θ.
因为
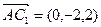
设G(0,2,h),则

∴-1×0+1×(-2)+2h="0. " ∴h=1,即G是AA1的中点.
(Ⅱ)设
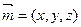 是平面EFG的法向量,则
是平面EFG的法向量,则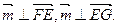
所以
 平面EFG的一个法向量m=(1,0,1)
平面EFG的一个法向量m=(1,0,1)∵

∴
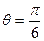 ,即AC1与平面EFG所成角
,即AC1与平面EFG所成角 为
为
解法二:(Ⅰ)取AC的中点D,连结DE、DG,则ED//BC
|
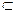 平面ABC,∴CC1⊥ED.
平面ABC,∴CC1⊥ED.∵CC1∩AC=C,∴ED⊥平面A1ACC1.
又∵AC1⊥EG,∴AC1⊥DG.
连结A1C,∵AC1⊥A1C,∴A1C//DG.
∵D是AC的中点,∴G是AA1的中点.
(Ⅱ)取CC1的中点M,连结GM、FM,则EF//GM,
∴E、F、M、G共面.作C1H⊥FM,交FM的延长线于H,∵AC⊥平面BB1C1C,
C1H
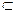 平面BB1C1C,∴AC⊥G1H,又AC//GM,∴GM⊥C1H. ∵GM∩FM=M,
平面BB1C1C,∴AC⊥G1H,又AC//GM,∴GM⊥C1H. ∵GM∩FM=M,∴C1H⊥平面EFG,设AC1与MG相交于N点,所以∠C1NH为直线AC1与平面EFG所成角θ.
因为


练习册系列答案
相关题目
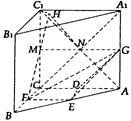
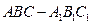 中,侧棱垂直于底面,底面△ABC中
中,侧棱垂直于底面,底面△ABC中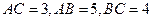 ,
,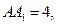 点
点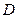 是
是 的中点。
的中点。
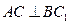

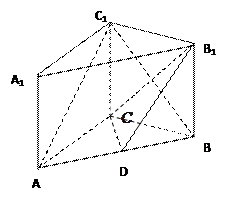
 。
。
 ,俯视图中
,俯视图中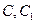 分别是所在边的中点,设
分别是所在边的中点,设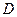 为
为 的中点.
的中点.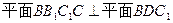 ;
;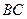 边上是否存在点
边上是否存在点 ,使
,使 ?若不存在,说明理由;若存在,请证明你的结论.
?若不存在,说明理由;若存在,请证明你的结论.
 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点. ,
,

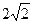 ,M为BC的中点
,M为BC的中点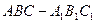 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱 的中点,平面ABD和平面
的中点,平面ABD和平面 的交线为MN.
的交线为MN. ;
; 所成的角为
所成的角为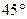 ,试求二面角
,试求二面角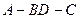 的大小.
的大小.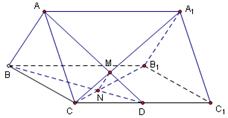
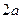 ,DC=
,DC= , F是BE的中点。
, F是BE的中点。
 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.