题目内容
设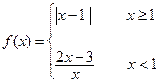 ,解不等式
,解不等式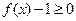 .
.
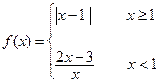 ,解不等式
,解不等式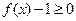 .
.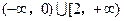
(1)当 时,原不等式等价于
时,原不等式等价于 ,即
,即 或
或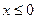
∴ .
.
(2)当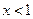 时,原不等式等价于
时,原不等式等价于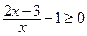 ,即
,即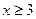 或
或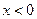
∴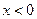 .
.
综上所述,不等式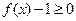 的解集为
的解集为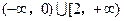 .
.
 时,原不等式等价于
时,原不等式等价于 ,即
,即 或
或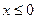
∴
 .
. (2)当
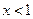 时,原不等式等价于
时,原不等式等价于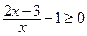 ,即
,即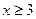 或
或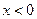
∴
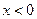 .
. 综上所述,不等式
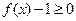 的解集为
的解集为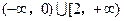 .
.
练习册系列答案
相关题目
题目内容
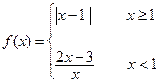 ,解不等式
,解不等式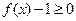 .
.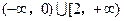
 时,原不等式等价于
时,原不等式等价于 ,即
,即 或
或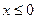
 .
. 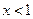 时,原不等式等价于
时,原不等式等价于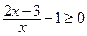 ,即
,即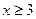 或
或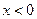
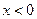 .
. 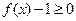 的解集为
的解集为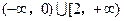 .
.