题目内容
如图所示,在正方体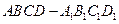 中,
中,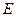 为
为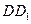 上的点、
上的点、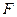 为
为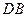 的中点.
的中点.
(Ⅰ)求直线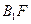 与平面
与平面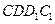 所成角的正弦值;
所成角的正弦值;
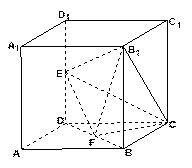 (Ⅱ)若直线
(Ⅱ)若直线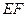 //平面
//平面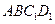 ,试确定点
,试确定点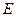 的位置.
的位置.
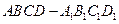 中,
中,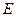 为
为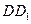 上的点、
上的点、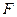 为
为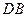 的中点.
的中点.(Ⅰ)求直线
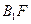 与平面
与平面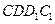 所成角的正弦值;
所成角的正弦值; (Ⅱ)若直线
(Ⅱ)若直线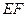 //平面
//平面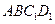 ,试确定点
,试确定点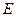 的位置.
的位置.(1)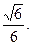 (2)中点
(2)中点
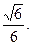 (2)中点
(2)中点(Ⅰ)∵平面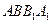 //平面
//平面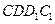
∴直线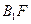 与平面
与平面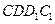 所成角等于直线
所成角等于直线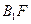 与平面
与平面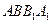 所成的角
所成的角
取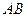 中点
中点 ,连接
,连接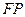 和
和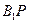
由已知可得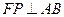 ,
,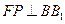 ,故
,故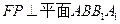
∴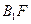 与平面
与平面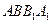 所成的角即为
所成的角即为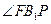
在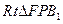 中,
中,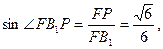 即
即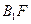 与平面
与平面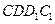 所成角的正弦值为
所成角的正弦值为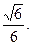 .
.
(Ⅱ)连接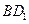 ,则平面
,则平面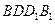 过
过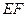 与平面
与平面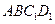 交于
交于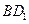
由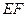 //平面
//平面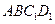 可得
可得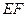 //
//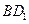
又因为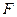 为
为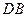 的中点
的中点
故得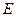 也必须为
也必须为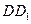 的中点.
的中点.
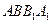 //平面
//平面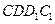
∴直线
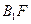 与平面
与平面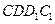 所成角等于直线
所成角等于直线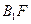 与平面
与平面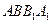 所成的角
所成的角取
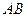 中点
中点 ,连接
,连接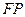 和
和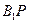
由已知可得
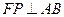 ,
,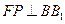 ,故
,故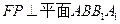
∴
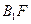 与平面
与平面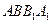 所成的角即为
所成的角即为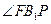
在
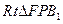 中,
中,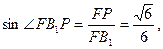 即
即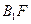 与平面
与平面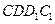 所成角的正弦值为
所成角的正弦值为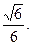 .
.(Ⅱ)连接
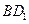 ,则平面
,则平面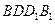 过
过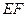 与平面
与平面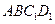 交于
交于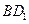
由
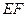 //平面
//平面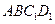 可得
可得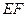 //
//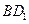
又因为
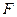 为
为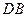 的中点
的中点故得
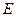 也必须为
也必须为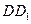 的中点.
的中点.
练习册系列答案
相关题目
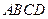 中,
中,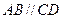 ,
,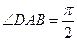 ,点
,点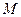 、
、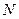 分别在
分别在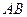 ,
,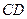 上,且
上,且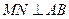 ,
,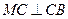 ,
,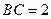 ,
,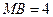 ,现将梯形
,现将梯形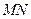 折起,使平面
折起,使平面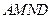 与平面
与平面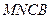 垂直(如图乙).
垂直(如图乙).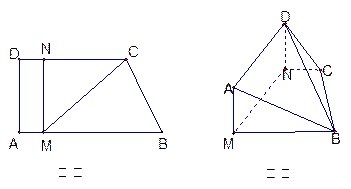
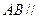 平面
平面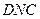 ;
;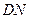 的长为何值时,
的长为何值时,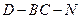 的大小为
的大小为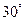 ?
?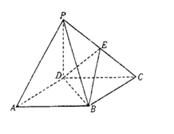
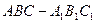 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱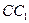 的中点,平面ABD和平面
的中点,平面ABD和平面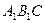 的交线为MN.
的交线为MN.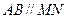 ;
;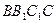 所成的角为
所成的角为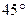 ,试求二面角
,试求二面角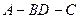 的大小.
的大小.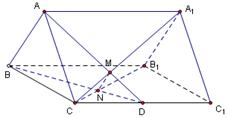
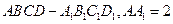 ,
, 为棱
为棱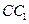 的中点.
的中点.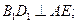
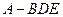 的体积;
的体积;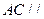 平面
平面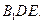 .
. 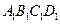 的棱长为l,点F为
的棱长为l,点F为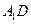 的中点.
的中点.
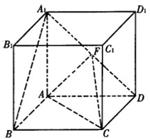
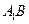 ∥平面AFC;.
∥平面AFC;.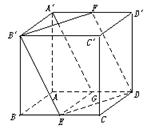
 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.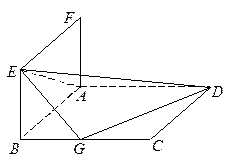
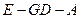 的正切值.
的正切值.