题目内容
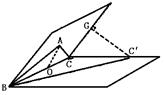
已知直角梯形ABCD中，AD∥BC，AB⊥AD，∠C=45°,AD=AB=2,把梯形沿BD折起成60°的二面角C′-BD-A.求： (1)C′到平面ADB的距离；
(2)AC′与BD所成的角.
(2)AC′与BD所成的角.
（1）
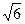（2）∠GAC′=60°
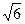（2）∠GAC′=60°(1)过C′作C′G⊥面BAD于G，连结DG.
∵AD="BA=2 " AD⊥AB
∴∠ADB=45°
又∵∠ADC=180°-45°=135°
∴∠BDC=135°-45°=90°
即BD⊥DC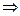
BD⊥DC′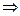BG⊥BD ∴∠GDC′=60°
C′G为所求
C′G=C′D·sib60°=2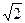
·
=
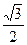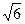
(2)DG=C′D·cos60°=2·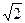
=
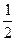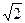
又AD="2 " A到BD的距 离AO=AD·sin45°=2α×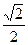
=
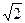
∴AG∥OD，即AG⊥DG，∠GAC′为所求.
tan∠GAC′=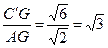
∴∠GAC′=60°
∵AD="BA=2 " AD⊥AB
∴∠ADB=45°
又∵∠ADC=180°-45°=135°
∴∠BDC=135°-45°=90°
即BD⊥DC
BD⊥DC′BG⊥BD ∴∠GDC′=60°C′G为所求
C′G=C′D·sib60°=2
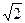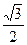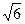
·=(2)DG=C′D·cos60°=2
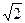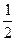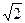
·= 又AD="2 " A到BD的距 离AO=AD·sin45°=2α×
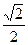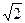
= ∴AG∥OD，即AG⊥DG，∠GAC′为所求.
tan∠GAC′=
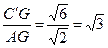
∴∠GAC′=60°
练习册系列答案
相关题目
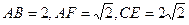，CE//AF，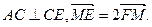
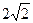，M为BC的中点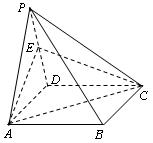
中,
,
.
;
的大小.
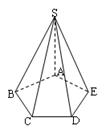
如图，PC⊥平面ABC，PM∥CB，∠ACB＝120°，PM＝AC＝1，BC＝2，异面直线AM与直线PC所成的角为60°.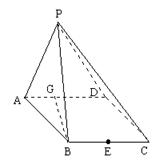
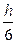（S上底面+4S中截面+S下底面），试判断V估与V的大小关系，并加以证明。
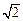，BB1＝3，D为A1C1的中点，F在线段AA1上．