Question

1．在如图所示的直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD是边长为2的菱形，且∠BAD=60°，AA₁=4．

（1）求直四棱柱ABCD-A₁B₁C₁D₁的体积；
（2）求异面直线AD₁与BA₁所成角的大小．

Answer 1

分析 （1）根据体积公式得出：菱形ABCD的面积×h即可，关键求面积，高．
（2）根据性质得出：∠A₁BC₁等于异面直线AD₁与BA₁所成角．在△A₁BC₁中，由余弦定理可求解．

解答 解：（1）因菱形ABCD的面积为AB²•sin60°=$2\sqrt{3}$
故直四棱柱ABCD-A₁B₁C₁D₁的体积为：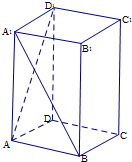

S_底面ABCD•AA₁=$2\sqrt{3}×4=8\sqrt{3}$     
（2）连接BC₁，A₁C₁，易知BC₁∥AD₁，
故∠A₁BC₁等于异面直线AD₁与BA₁所成角．
由已知，可得A₁B=BC₁=$2\sqrt{5}$，A₁C₁=$2\sqrt{3}$                     
则在△A₁BC₁中，由余弦定理，得cos∠A₁BC₁=$\frac{{A}_{1}{B}^{2}+B{C}_{1}^{2}-{A}_{1}{{C}_{1}}^{2}}{2{A}_{1}B•B{C}_{1}}$=$\frac{7}{10}$   
故异面直线AD₁与BA所成角的大小为arcos$\frac{7}{10}$

点评 本题考查了空间几何体的性质，运用求解体积，空间想象能力，思维能力的运用，属于中档题．