题目内容
14．
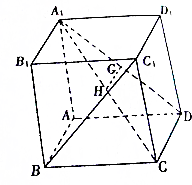如图，正方体ABCD-A1B1C1D1的棱长为1，G，H分别为DA1，CA1中点（1）求证：GH∥平面CDD1C1
（2）求证：BC1⊥平面A1CD
（3）求三棱锥A-BCG的体积．
分析 （1）利用三角形的中位线的性质，证明GH∥CD，即可证明GH∥平面CDD1C1
（2）连接B1C，证明：BC1⊥平面A1B1CD，即可证明BC1⊥平面A1CD
（3）三棱锥A-BCG的体积，等于三棱锥G-ABC的体积．
解答 （1）证明：∵G，H分别为DA1，CA1中点，
∴GH∥CD，
∵GH?平面CDD1C1，CD?平面CDD1C1，
∴GH∥平面CDD1C1
（2）证明：连接B1C，则B1C⊥BC1，
∵BC1⊥CD，CD∩B1C=C，
∴BC1⊥平面A1B1CD
即BC1⊥平面A1CD；
（3）解：三棱锥A-BCG的体积，等于三棱锥G-ABC的体积，即$\frac{1}{3}×\frac{1}{2}×1×1×\frac{1}{2}$=$\frac{1}{12}$．
点评 本题考查线面平行与垂直，考查三棱锥A-BCG的体积，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
7．正△ABC边长为1，P为其内部（不含边界）的任意点，设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$（x，y∈R），则在平面直角坐标系内点（x，y）对应区域的面积为（ ）
| A． | 1 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{4}$ |