题目内容
9.已知点A(1,3),B(3,6),点P在直线y=x+1上,求|PA|+|PB|的最小值,以及取最小值时P点的坐标.分析 设点A(1,3)关于直线y=x+1的对称点A′(m,n).利用轴对称的性质可得A′的坐标.连接A′B与直线相交于点P,则|PA|+|PB|的最小值为|A′B|.利用两点间的距离公式即可得出|PA|+|PB|的最小值,求出A′B方程,与y=x+1联立,可得P的坐标.
解答 解:设点A(1,3)关于直线y=x+1的对称点A′(m,n).
则$\left\{\begin{array}{l}{\frac{n+3}{2}=\frac{m+1}{2}+1}\\{\frac{n-3}{m-1}=-1}\end{array}\right.$,
解得m=2,n=2,
连接A′B与直线相交于点P,则|PA|+|PB|的最小值为|A′B|=$\sqrt{(3-2)^{2}+(6-2)^{2}}$=$\sqrt{17}$.
A′B方程为y-2=$\frac{6-2}{3-2}$(x-2),即4x-y-6=0,
与y=x+1联立,可得P的坐标为($\frac{7}{3}$,$\frac{10}{3}$).
点评 本题考查了最小值问题转化为轴对称问题,考查了相互垂直的直线斜率之间的关系和中点坐标公式,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
5.如果方程x2+$\frac{{y}^{2}}{k}$=2表示焦点在x轴上的椭圆,那么实数k的取值范围是( )
| A. | (0,2) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
3.由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{lnx-y+1≥0}\\{2x-(e-1)y-2≤0}\end{array}\right.$确定的平面区域为M,由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{0≤y≤2}\end{array}\right.$确定的平面区域为N,在N内随机的取一点P,则点P落在区域M内的概率为( )
| A. | $\frac{1}{2e-2}$ | B. | $\frac{e-2}{2e-2}$ | C. | $\frac{3-e}{4e-4}$ | D. | $\frac{e}{2e-2}$ |
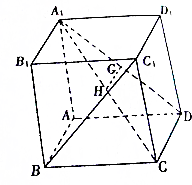 如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点
如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点