题目内容
8.已知P1,P2,…P2015是抛物线y2=4x上的点,它们的横坐标依次为x1,x2,…,x2015,F是抛物线的焦点,若x1+x2+…+x2015=10,则|P1F|+|P2F|+…+|P2015F|=( )| A. | 2015 | B. | 2025 | C. | 4030 | D. | 4040 |
分析 根据抛物线的定义得抛物线上的点到焦点的距离等于该点到准线的距离,因此求出抛物线的准线方程,结合题中数据加以计算,即可得到本题答案.
解答 解:∵抛物线y2=4x的焦点为F(1,0),准线为x=-1,
∴根据抛物线的定义,Pi(i=1,2,3,…,2015)到焦点的距离等于Pi到准线的距离,即|PiF|=xi+1,
可得|P1F|+|P2F|+…|P2015F|=(x1+1)+(x2+1)+…+(x2015+1)=(x1+x2+…+x2015)+2015,
∵x1+x2+…+x2015=10,
∴|P1F|+|P2F|+…|P2015F|=10+2015=2025.
故选:B.
点评 本题给出抛物线上2015个点的横坐标之和,求它们到焦点的距离之和.着重考查了抛物线的定义、标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
19.${∫}_{-\frac{π}{3}}^{\frac{π}{3}}$cosxdx=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
3.由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{lnx-y+1≥0}\\{2x-(e-1)y-2≤0}\end{array}\right.$确定的平面区域为M,由不等式组$\left\{\begin{array}{l}{1≤x≤e}\\{0≤y≤2}\end{array}\right.$确定的平面区域为N,在N内随机的取一点P,则点P落在区域M内的概率为( )
| A. | $\frac{1}{2e-2}$ | B. | $\frac{e-2}{2e-2}$ | C. | $\frac{3-e}{4e-4}$ | D. | $\frac{e}{2e-2}$ |
18.正项等比数列{an}中的a1,a9是函数f(x)=$\frac{1}{3}{x^3}-a{x^2}$+x+1的极值点,则lna5=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 与a的值有关 |
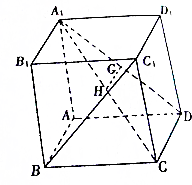 如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点
如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点