题目内容
3.已知椭圆C1的中心在坐标原点,两个焦点分别为F1(-2,0),F2(2,0),点A(2,3)在椭圆C1上,过点A的直线L与抛物线C2:x2=4y交于B,C两点,抛物线C2在点B,C处的切线分别为l1,l2,且l1与l2交于点P.(Ⅰ) 求椭圆C1的方程;
(Ⅱ)是否存在满足|PF1|+|PF2|=|AF1|+|AF2|的点P?若存在,指出这样的点P有几个(不必求出点P的坐标); 若不存在,说明理由.
分析 (Ⅰ)设椭圆C1的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由c=2,$\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}$=1,a2=b2+c2,联立解得即可得出.
(II)设B(x1,y1),C(x2,y2),P(x0,y0).设直线AB的方程为:y-3=k(x-2),与抛物线方程联立化为x2-4kx+8k-12=0.由抛物线C2:x2=4y,可得${y}^{′}=\frac{1}{2}x$.可得 C2在点B处的切线l1的方程为:$y=\frac{1}{2}{x}_{1}•x-\frac{1}{4}{x}_{1}^{2}$.C2在点C处的切线l2的方程为:$y=\frac{{x}_{2}}{2}x-\frac{1}{4}{x}_{2}^{2}$.联立P(2k,2k-3).由于|PF1|+|PF2|=|AF1|+|AF2|,可得点P在椭圆C1:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$上.代入可得7k2-12k-3=0.由△1>0,可得方程有两个不等的实数根.
解答 解:(Ⅰ)设椭圆C1的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由c=2,$\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}$=1,a2=b2+c2,
联立解得a2=16,b2=12.
∴椭圆C1的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
(Ⅱ)设B(x1,y1),C(x2,y2),P(x0,y0).
设直线AB的方程为:y-3=k(x-2),联立$\left\{\begin{array}{l}{y=kx+3-2k}\\{{x}^{2}=4y}\end{array}\right.$,化为x2-4kx+8k-12=0.
△=16k2-4(8k-12)>0.
∴x1+x2=4k,x1x2=8k-12.
由抛物线C2:x2=4y,可得${y}^{′}=\frac{1}{2}x$.
∴C2在点B处的切线l1的方程为:$y=\frac{1}{2}{x}_{1}•x-\frac{1}{4}{x}_{1}^{2}$..
同理C2在点C处的切线l2的方程为:$y=\frac{{x}_{2}}{2}x-\frac{1}{4}{x}_{2}^{2}$.
联立$\left\{\begin{array}{l}{y=\frac{{x}_{1}}{2}x-\frac{1}{4}{x}_{1}^{2}}\\{y=\frac{{x}_{2}}{2}x-\frac{1}{4}{x}_{2}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{2}=2k}\\{y=\frac{{x}_{1}{x}_{2}}{4}=2k-2}\end{array}\right.$,∴P(2k,2k-3).
∵|PF1|+|PF2|=|AF1|+|AF2|,
∴点P在椭圆C1:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$上.
∴$\frac{(2k)^{2}}{16}+\frac{(2k-3)^{2}}{12}=1$.
化简得7k2-12k-3=0.(*)
由△1=122+4×21>0,可得方程(*)有两个不等的实数根.
∴满足条件的点P有两个.
点评 本题考查了椭圆与抛物线的标准方程及其性质、直线与抛物线相交转化为方程联立可得根与系数的关系、直线与抛物线相切切线问题、导数的几何意义,考查了推理能力与计算能力,属于难题

 阅读快车系列答案
阅读快车系列答案| A. | [0,1] | B. | [1,3] | C. | [2,4] | D. | [3,4] |
| A. | a,b,c,d全都大于等于0 | B. | a,b,c,d全为正数 | ||
| C. | a,b,c,d中至少有一个正数 | D. | a,b,c,d中至多有一个负数 |
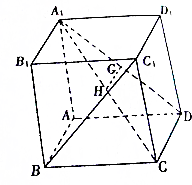 如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点
如图,正方体ABCD-A1B1C1D1的棱长为1,G,H分别为DA1,CA1中点