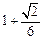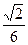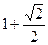题目内容
(本小题满分15分)
(文)已知直线
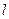 与曲线
与曲线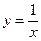 相切,分别求
相切,分别求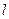 的方程,使之满足:
的方程,使之满足:(1)
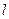 经过点
经过点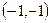 ;(2)
;(2)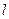 经过点
经过点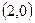 ;(3)
;(3)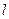 平行于直线
平行于直线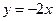 ;
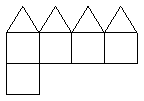
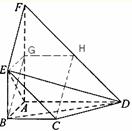
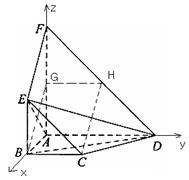
;(理)如图,平面
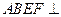 平面
平面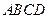 ,四边形
,四边形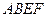 与
与 都是直角梯形,
都是直角梯形,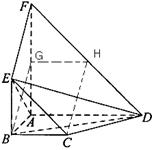
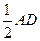 ,
,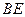
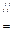
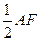 ,
,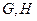 分别为
分别为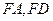 的中点
的中点(Ⅰ)证明:四边形
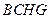 是平行四边形;
是平行四边形;(Ⅱ)
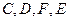 四点是否共面?为什么?
四点是否共面?为什么?(Ⅲ)设
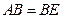 ,证明:平面
,证明:平面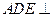 平面
平面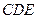 ;
;【解1】:(Ⅰ)由题意知,
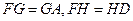
 所以
所以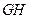
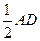
又
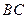
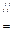
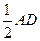 ,故
,故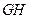
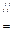
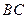
所以四边形
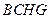 是平行四边形。
是平行四边形。(Ⅱ)
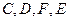 四点共面。理由如下:
四点共面。理由如下:由
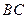
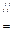
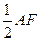 ,
,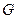 是
是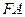 的中点知,
的中点知,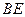
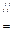
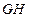 ,所以
,所以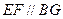
由(Ⅰ)知
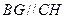 ,所以
,所以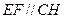 ,故
,故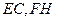 共面。又点
共面。又点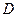 在直线
在直线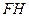 上
上所以
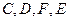 四点共面。
四点共面。(Ⅲ)连结
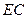 ,由
,由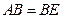 ,
,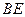
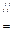
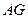 及
及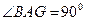 知
知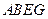 是正方形
是正方形故
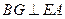 。由题设知
。由题设知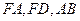 两两垂直,故
两两垂直,故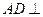 平面
平面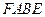 ,
,因此
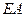 是
是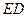 在平面
在平面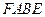 内的射影,根据三垂线定理,
内的射影,根据三垂线定理,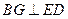
又
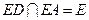 ,所以
,所以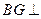 平面
平面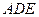
由(Ⅰ)知
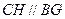 ,所以
,所以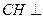 平面
平面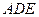 。
。由(Ⅱ)知
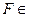 平面
平面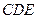 ,故
,故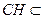 平面
平面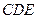 ,得平面
,得平面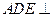 平面
平面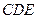
【解2】:由平面
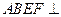 平面
平面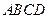 ,
,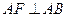 ,得
,得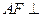 平面
平面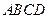 ,
,以
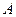 为坐标原点,射线
为坐标原点,射线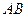 为
为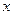 轴正半轴,建立如图所示的直角坐标系
轴正半轴,建立如图所示的直角坐标系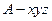
(Ⅰ)设
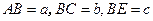 ,则由题设得
,则由题设得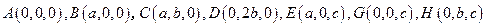
 所以
所以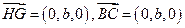
于是
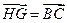
又点
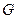 不在直线
不在直线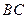 上
上所以四边形
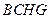 是平行四边形。
是平行四边形。(Ⅱ)
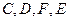 四点共面。理由如下:
四点共面。理由如下:由题设知
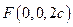 ,所以
,所以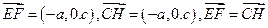
又
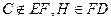 ,故
,故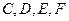 四点共面。
四点共面。(Ⅲ)由
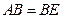 得,所以
得,所以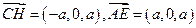
又
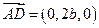 ,因此
,因此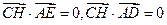
即
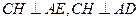
又
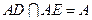 ,所以
,所以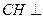 平面
平面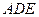
故由
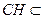 平面
平面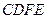 ,得平面
,得平面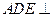 平面
平面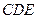

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
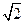 .
.
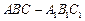 中,已知
中,已知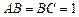 ,
,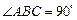 ,
,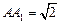 ,
,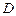 ,
,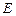 分别为
分别为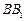 、
、 的中点.
的中点.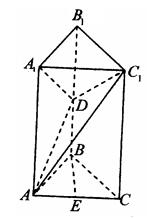
 平面
平面 ;(II)求二面角
;(II)求二面角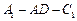 的大小.
的大小. 

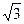 ,侧面PAD为等边三角形,并且与底面所成二面角为60
,侧面PAD为等边三角形,并且与底面所成二面角为60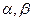 和两条不重合的直线
和两条不重合的直线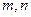 ,下列四个命题:
,下列四个命题: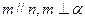 则
则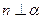 ②若
②若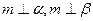 则
则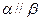
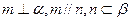 则
则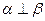 ④若
④若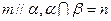 则
则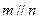
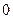 个
个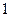 个
个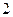 个
个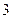 个
个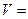 ( )
( )