题目内容
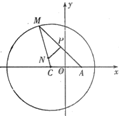
与y轴相切且和半圆x2+y2=4（0≤x≤2）内切的动圆圆心的轨迹方程是（ ）
| A．y2=4（x+1）（0＜x≤1） | B．y2=4（x-1）（0＜x≤1） |
| C．y2=-4（x-1）（0＜x≤1） | D．y2=-2（x-1）（0＜x≤1） |
设圆心为（x，y），则动圆的半径为x，
因为与已知圆内切，还要与y轴相切，所以可知x的范围为0＜x≤1．
同时原点到动圆圆心的距离为：
，
则由题意有下列方程：
x+
=2．
整理得y2=4-4x（0＜x≤1）．
所以动圆圆心的轨迹方程为：y2=4-4x（0＜x≤1）．
故选A．
因为与已知圆内切，还要与y轴相切，所以可知x的范围为0＜x≤1．
同时原点到动圆圆心的距离为：
| x2+y2 |
则由题意有下列方程：
x+
| x2+y2 |
整理得y2=4-4x（0＜x≤1）．
所以动圆圆心的轨迹方程为：y2=4-4x（0＜x≤1）．
故选A．
练习册系列答案
智能训练练测考系列答案
相关题目
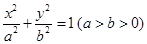过点
，
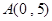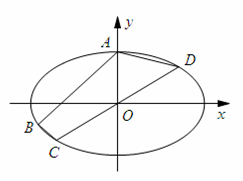
，C、D在该椭圆上，直线CD过原点O，且在线段AB的右下侧．
