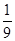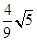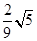题目内容
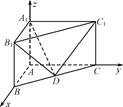
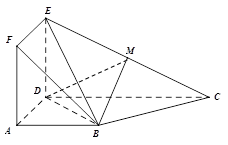
如图,边长为1的正三角形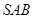 所在平面与直角梯形
所在平面与直角梯形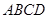 所在平面垂直,且
所在平面垂直,且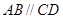 ,
,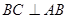 ,
,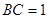 ,
,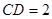 ,
, 、
、 分别是线段
分别是线段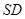 、
、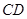 的中点.
的中点.
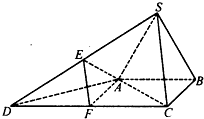
(1)求证:平面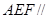 平面
平面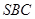 ;
;
(2)求二面角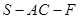 的余弦值.
的余弦值.
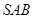 所在平面与直角梯形
所在平面与直角梯形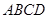 所在平面垂直,且
所在平面垂直,且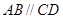 ,
,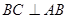 ,
,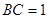 ,
,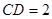 ,
,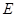 、
、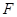 分别是线段
分别是线段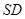 、
、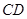 的中点.
的中点.
(1)求证:平面
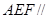 平面
平面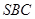 ;
;(2)求二面角
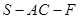 的余弦值.
的余弦值.(1)详见解析;(2)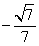 .
.
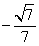 .
.试题分析:(1)由已知中F为CD的中点,易判断四边形ABCD为平行四边形,进而AF∥BC,同时EF∥SC,再由面面平行的判定定理,即可得到答案.(II)取AB的中点O,连接SO,以O为原点,建立如图所示的空间坐标系,分别求出平面SAC与平面ACF的法向量,代入向量夹角公式,即可求出二面角S-AC-F的大小..
(1)
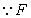 分别是
分别是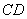 的中点,
的中点,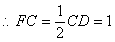 .又
.又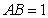 ,所以
,所以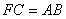 .
.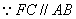 ,……2分
,……2分 四边形
四边形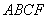 是平行四边形.
是平行四边形.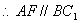 .
.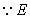 是
是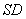 的中点,
的中点,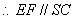 .……3分
.……3分又
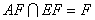 ,
,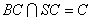 ,
, 平面
平面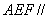 平面
平面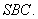 ……5分
……5分(2)取
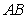 的中点
的中点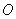 ,连接
,连接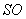 ,则在正
,则在正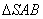 中,
中,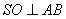 ,又
,又 平面
平面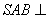 平面
平面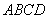 ,
,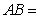 平面
平面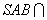 平面
平面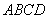 ,
,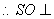 平面
平面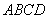 .…6分
.…6分于是可建立如图所示的空间直角坐标系
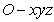 .
.
则有
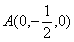 ,
,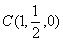 ,
,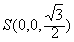 ,
,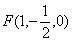 ,
,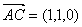 ,
,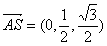 .…7分
.…7分设平面
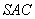 的法向量为
的法向量为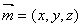 ,由
,由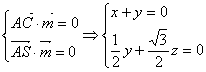 .
.取
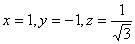 ,得
,得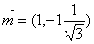 .……9分平面
.……9分平面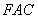 的法向量为
的法向量为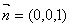 .10分
.10分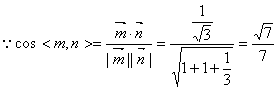 …11分而二面角
…11分而二面角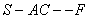 的大小为钝角,
的大小为钝角, 二面角
二面角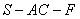 的余弦值为
的余弦值为 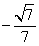 .
.
练习册系列答案
相关题目
 与梯形
与梯形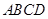 所在的平面互相垂直,
所在的平面互相垂直,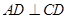 ,
,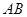 ∥
∥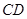 ,
,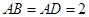 ,
,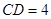 ,
,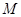 为
为 的中点.
的中点.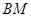 ∥平面
∥平面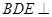 平面
平面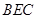 ;
;
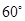 ,∠BAC
,∠BAC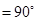 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC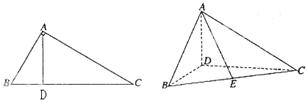
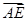 与
与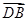 夹角的余弦值.
夹角的余弦值.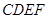 为正方形,面
为正方形,面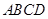 为等腰梯形,
为等腰梯形,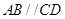 ,
,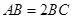 ,
,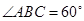 ,且平面
,且平面 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值;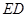 上是否存在点
上是否存在点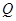 ,使平面
,使平面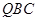 ?
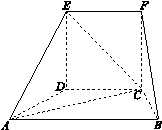
?
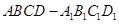 中,
中,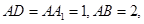 点
点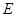 在棱
在棱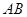 上.
上.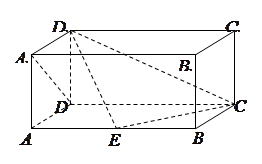
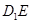 与
与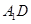 所成的角;
所成的角;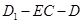 的大小为
的大小为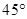 ,求点
,求点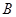 到平面
到平面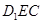 的距离.
的距离.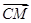 ,
,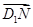 〉的值为( )
〉的值为( )