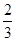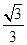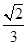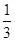题目内容
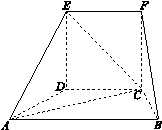
如图所示的几何体中,面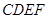 为正方形,面
为正方形,面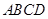 为等腰梯形,
为等腰梯形,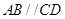 ,
,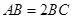 ,
,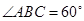 ,且平面
,且平面
 平面
平面 .
.
(1)求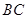 与平面
与平面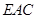 所成角的正弦值;
所成角的正弦值;
(2)线段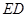 上是否存在点
上是否存在点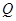 ,使平面
,使平面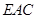
 平面
平面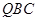 ?
?
证明你的结论.
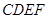 为正方形,面
为正方形,面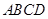 为等腰梯形,
为等腰梯形,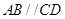 ,
,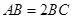 ,
,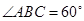 ,且平面
,且平面
 平面
平面 .
.(1)求
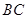 与平面
与平面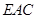 所成角的正弦值;
所成角的正弦值;(2)线段
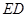 上是否存在点
上是否存在点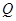 ,使平面
,使平面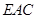
 平面
平面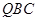 ?
?证明你的结论.

(1)  , (2)详见解析.
, (2)详见解析.
 , (2)详见解析.
, (2)详见解析.试题分析:(1)利用空间向量求线面角,关键求出面的一个法向量. 先由面面垂直得到线面垂直,即由平面
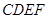
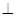 面
面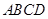 ,得
,得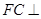 平面
平面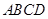 .建立空间直角坐标系,表示各点坐标,得
.建立空间直角坐标系,表示各点坐标,得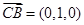 ,设平面
,设平面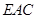 的法向量为
的法向量为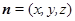 ,则有
,则有 所以
所以 取
取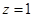 ,得
,得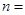
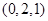 .根据
.根据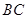 与平面
与平面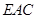 所成的角正弦值等于
所成的角正弦值等于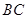 与平面
与平面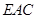 法向量夹角余弦值的绝对值,得到
法向量夹角余弦值的绝对值,得到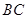 与平面
与平面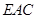 所成角的正弦值为
所成角的正弦值为 .(2) 假设线段
.(2) 假设线段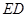 上存在点
上存在点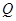 ,设
,设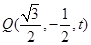
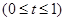 ,可求出平面
,可求出平面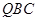 的一个法向量
的一个法向量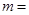
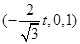 .要使平面
.要使平面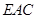
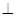 平面
平面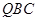 ,只需
,只需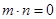 ,即
,即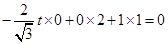 ,此方程无解,所以线段
,此方程无解,所以线段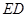 上不存在点
上不存在点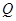 ,使平面
,使平面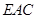
 平面
平面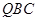 .
.(1)因为
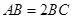 ,
,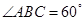 ,
,在△
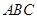 中,由余弦定理可得
中,由余弦定理可得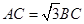 ,
,所以
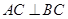 . 又因为
. 又因为
平面
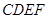
 面
面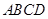 ,所以
,所以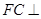 平面
平面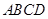 .
. 所以
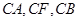 两两互相垂直,
两两互相垂直,如图建立空间直角坐标系
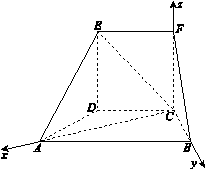
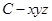 .
.
设
 ,所以
,所以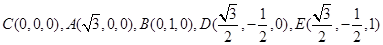 .
.所以
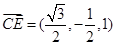 ,
,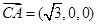 ,
,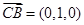 .
.设平面
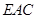 的法向量为
的法向量为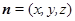 ,则有
,则有
所以
 取
取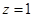 ,得
,得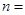
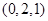 .
. 设
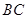 与平面
与平面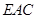 所成的角为
所成的角为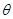 ,则
,则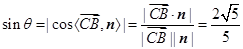 ,
,所以
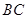 与平面
与平面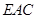 所成角的正弦值为
所成角的正弦值为 .
.(2)线段
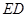 上不存在点
上不存在点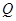 ,使平面
,使平面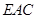
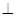 平面
平面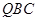 .证明如下:
.证明如下:假设线段
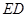 上存在点
上存在点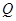 ,设
,设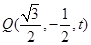
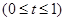 ,所以
,所以 .
.设平面
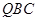 的法向量为
的法向量为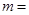
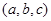 ,则有
,则有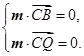
所以
 取
取 ,得
,得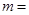
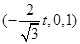 .
.要使平面
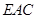
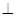 平面
平面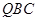 ,只需
,只需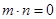 ,即
,即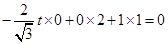 ,
,此方程无解,所以线段
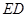 上不存在点
上不存在点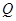 ,使平面
,使平面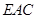
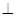 平面
平面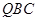 .
.
练习册系列答案
相关题目
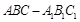 中,
中,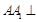 底面
底面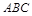 ,
,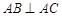 ,
,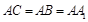 ,
,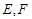 分别是棱
分别是棱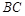 ,
,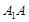 的中点,
的中点,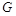 为棱
为棱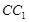 上的一点,且
上的一点,且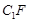 //平面
//平面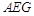 .
.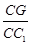 的值;
的值;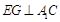 ;
;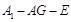 的余弦值.
的余弦值.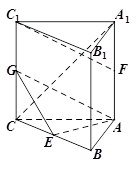
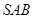 所在平面与直角梯形
所在平面与直角梯形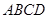 所在平面垂直,且
所在平面垂直,且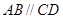 ,
,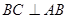 ,
,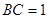 ,
,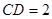 ,
,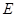 、
、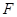 分别是线段
分别是线段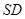 、
、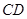 的中点.
的中点.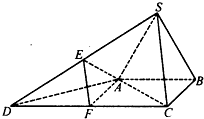
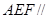 平面
平面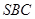 ;
;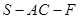 的余弦值.
的余弦值.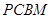 是直角梯形,∠
是直角梯形,∠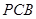 =90°,
=90°,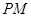 ∥
∥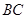 ,
,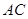 =1,∠
=1,∠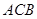 =120°,
=120°,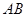 ⊥
⊥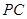 ,直线
,直线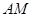 与直线
与直线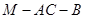 的的余弦值;
的的余弦值;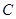 到面
到面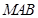 的距离.
的距离.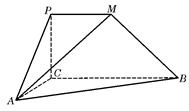
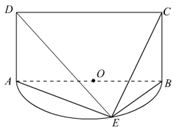
 是以
是以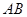 为直径的半圆
为直径的半圆 上异于
上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆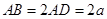 .
.
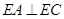 ;
;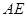 和
和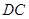 所成的角为
所成的角为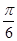 ,求平面
,求平面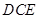 与平面
与平面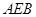 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.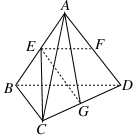
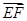 ·
·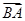 ;
;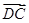 ;
;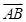 ,
,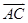 为边的平行四边形的面积;
为边的平行四边形的面积;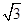 ,且a分别与
,且a分别与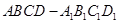 中
中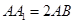 ,则
,则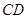 与平面
与平面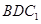 所成角的正弦值等于( )
所成角的正弦值等于( )