题目内容
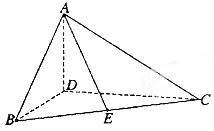
如图,在△ABC中,∠ABC=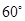 ,∠BAC
,∠BAC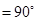 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC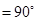 .
.
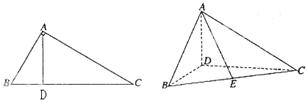
(1)证明:平面ADB⊥平面BDC;
(2)设E为BC的中点,求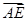 与
与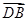 夹角的余弦值.
夹角的余弦值.
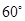 ,∠BAC
,∠BAC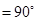 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC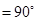 .
.
(1)证明:平面ADB⊥平面BDC;
(2)设E为BC的中点,求
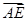 与
与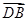 夹角的余弦值.
夹角的余弦值.(1)见解析 (2)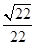
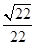
(1)确定图形在折起前后的不变性质,如角的大小不变,线段长度不变,线线关系不变,再由面面垂直的判定定理进行推理证明;(2)在(1)的基础上确定出三线两两垂直,建立空间直角坐标系,利用向量的坐标和向量的数量积运算求解.
(1)∵折起前AD是BC边上的高,
∴当△ABD折起后, AD⊥DC,AD⊥DB,
又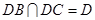 ,∴AD⊥平面BDC,
,∴AD⊥平面BDC,
∵AD 平面ABD,∴平面ABD⊥平面BDC.
平面ABD,∴平面ABD⊥平面BDC.
(2)由∠BDC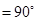 及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以
及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以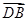 ,
,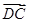 ,
,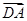 所在直线为
所在直线为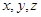 轴建立如图所示的空间直角坐标系,易得:
轴建立如图所示的空间直角坐标系,易得:
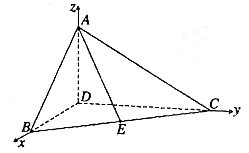
D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,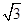 ),E(
),E(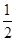 ,
,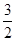 ,0),
,0),
所以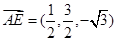 ,
,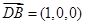 ,
,
∴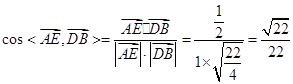
所以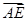 与
与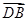 夹角的余弦值是
夹角的余弦值是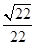 .
.

(1)∵折起前AD是BC边上的高,
∴当△ABD折起后, AD⊥DC,AD⊥DB,
又
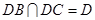 ,∴AD⊥平面BDC,
,∴AD⊥平面BDC,∵AD
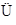 平面ABD,∴平面ABD⊥平面BDC.
平面ABD,∴平面ABD⊥平面BDC.(2)由∠BDC
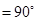 及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以
及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以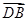 ,
,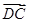 ,
,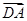 所在直线为
所在直线为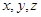 轴建立如图所示的空间直角坐标系,易得:
轴建立如图所示的空间直角坐标系,易得:
D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,
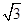 ),E(
),E(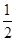 ,
,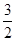 ,0),
,0),所以
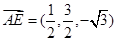 ,
,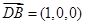 ,
,∴
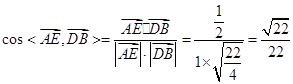
所以
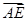 与
与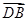 夹角的余弦值是
夹角的余弦值是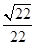 .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 中,底面
中,底面 是直角梯形,
是直角梯形,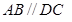 ,
, ,
,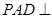 平面
平面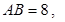
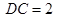 ,
,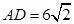 ,
, ,
, ,且
,且 .
.
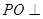 平面
平面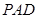 与平面
与平面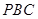 所成二面角的大小为
所成二面角的大小为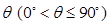 ,求
,求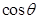 的值.
的值.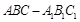 中,
中,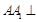 底面
底面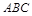 ,
,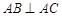 ,
,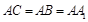 ,
,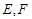 分别是棱
分别是棱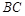 ,
,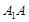 的中点,
的中点,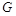 为棱
为棱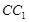 上的一点,且
上的一点,且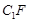 //平面
//平面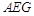 .
.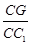 的值;
的值;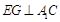 ;
; 的余弦值.
的余弦值.
 所在平面与直角梯形
所在平面与直角梯形 所在平面垂直,且
所在平面垂直,且 ,
,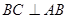 ,
,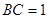 ,
,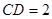 ,
,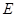 、
、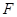 分别是线段
分别是线段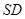 、
、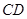 的中点.
的中点.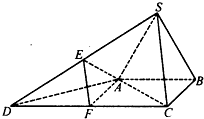
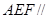 平面
平面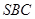 ;
;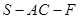 的余弦值.
的余弦值.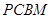 是直角梯形,∠
是直角梯形,∠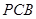 =90°,
=90°,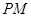 ∥
∥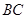 ,
,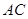 =1,∠
=1,∠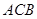 =120°,
=120°,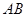 ⊥
⊥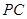 ,直线
,直线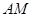 与直线
与直线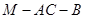 的的余弦值;
的的余弦值;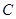 到面
到面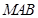 的距离.
的距离.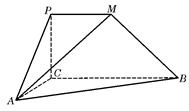
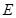 是以
是以 为直径的半圆
为直径的半圆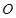 上异于
上异于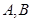 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆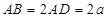 。
。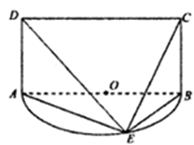
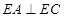 。
。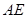 和
和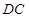 所成的角为
所成的角为 ,求平面
,求平面 和平面
和平面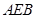 所成的锐二面角的余弦值。
所成的锐二面角的余弦值。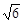 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记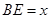 ,用
,用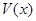 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.
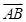 ,
,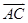 为边的平行四边形的面积;
为边的平行四边形的面积;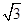 ,且a分别与
,且a分别与