题目内容
12.将正整数1,2,3,…按照如图的规律排列,则200应在第20列.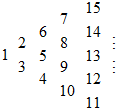
分析 先找到数的分布规律,求出第n列结束的时候一共出现的数的个数,每一列的数字都是从大大小按排列的,且每一列的数字个数等于列数,继而求出答案.
解答 解:由排列的规律可得,第n列有n个数,
则第n列结束的时候排了1+2+3+…+n-1=$\frac{1}{2}$n(n+1)个数.
则当n=19时,$\frac{1}{2}$n(n+1)=$\frac{1}{2}$×19×20=190,
则当n=20时,$\frac{1}{2}$n(n+1)=$\frac{1}{2}$×20×21=210,
∴故200应在第20列.
故答案为:20
点评 此题主要考查了数字的变化规律,借助于一个三角形数阵考查数列的应用,比较基础.

练习册系列答案
相关题目
20.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=2$\overrightarrow{DB}$,则$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$其中m,n分别为( )
| A. | m=$\frac{1}{3}$,n=-$\frac{2}{3}$ | B. | m=$\frac{1}{3}$,n=$\frac{2}{3}$ | C. | m=-$\frac{2}{3}$,n=$\frac{1}{3}$ | D. | m=$\frac{2}{3}$,n=$\frac{1}{3}$ |
2.如框图,当x1=5,x2=8,p=8.5时,x3=( )
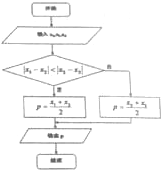

| A. | 6 | B. | 7 | C. | 9 | D. | 10 |