题目内容
10.设两圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|的值为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 8$\sqrt{2}$ | D. | 8 |
分析 圆在第一象限内,设圆心的坐标为(a,a),则有|a|=$\sqrt{(a-4)^{2}+(a-1)^{2}}$,解方程求得a值,代入两点间的距离公式可求得两圆心的距离|C1C2|的值.
解答 解:∵两圆C1、C2都和两坐标轴相切,且都过点(4,1),故圆在第一象限内,
设圆心的坐标为(a,a),则有|a|=|=$\sqrt{(a-4)^{2}+(a-1)^{2}}$,
∴a=5+2$\sqrt{2}$,或 a=5-2$\sqrt{2}$,故圆心为(5+2$\sqrt{2}$,5+2$\sqrt{2}$ ) 和 (5-2$\sqrt{2}$,5-2$\sqrt{2}$),
故两圆心的距离|C1C2|=$\sqrt{(4\sqrt{2})^{2}+(4\sqrt{2})^{2}}$=8,
故选:D.
点评 本题考查直线和圆相切的性质,点到直线的距离公式的应用,属于基础题

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
20.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=2$\overrightarrow{DB}$,则$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$其中m,n分别为( )
| A. | m=$\frac{1}{3}$,n=-$\frac{2}{3}$ | B. | m=$\frac{1}{3}$,n=$\frac{2}{3}$ | C. | m=-$\frac{2}{3}$,n=$\frac{1}{3}$ | D. | m=$\frac{2}{3}$,n=$\frac{1}{3}$ |
15.等比数列{an}中,a1=1,a5=4,则a3=( )
| A. | ±2 | B. | 2 | C. | -2 | D. | ±$\sqrt{2}$ |
2.如框图,当x1=5,x2=8,p=8.5时,x3=( )
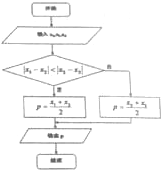

| A. | 6 | B. | 7 | C. | 9 | D. | 10 |
19.数列{an}满足a1=1,an+1=an-3(n∈N*),则a4=( )
| A. | 10 | B. | 8 | C. | -8 | D. | -10 |