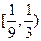题目内容
已知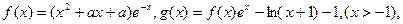
(1)当a=1时,试求函数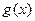 的单调区间,并证明此时方程
的单调区间,并证明此时方程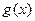 =0只有一个实数根,并求出此实数根;
=0只有一个实数根,并求出此实数根;
(2)证明: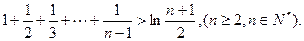
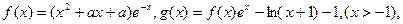
(1)当a=1时,试求函数
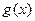 的单调区间,并证明此时方程
的单调区间,并证明此时方程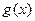 =0只有一个实数根,并求出此实数根;
=0只有一个实数根,并求出此实数根;(2)证明:
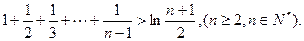
(1)(2)见解析
(1)当a=1时,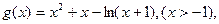
则 ,所以单调增区间为(0,+∞),令
,所以单调增区间为(0,+∞),令 ,所以单调减区间为(-1,0).2分
,所以单调减区间为(-1,0).2分
又 …4分
…4分
(2)
令
(i)当2-a=0即a=2时, 无极值,舍去.
无极值,舍去.
(ii)当2-a>0即a<2时, 的变化情况如下表(一):
的变化情况如下表(一):
由题意应有 满足题意………………………………8分
满足题意………………………………8分
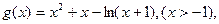
则
 ,所以单调增区间为(0,+∞),令
,所以单调增区间为(0,+∞),令 ,所以单调减区间为(-1,0).2分
,所以单调减区间为(-1,0).2分又
 …4分
…4分(2)

令

(i)当2-a=0即a=2时,
 无极值,舍去.
无极值,舍去.(ii)当2-a>0即a<2时,
 的变化情况如下表(一):
的变化情况如下表(一):| x | (-∞,0) | 0 | (0,2-a) | 2-a | (2-a,+∞) |
 | - | 0 | + | 0 | - |
 |  | 极小值 |  | 极大值 |  |
 满足题意………………………………8分
满足题意………………………………8分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,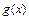 的图象与
的图象与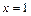 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,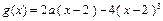 .
.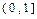 上为增函数,求
上为增函数,求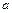 的取值范围;
的取值范围;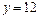 上?若存在,求出
上?若存在,求出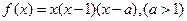
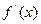 ; 并证明
; 并证明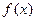 有两个不同的极值点
有两个不同的极值点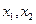 ;
; 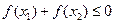 成立,求
成立,求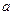 的取值范围.
的取值范围.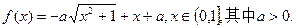
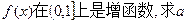 的取值范围;
的取值范围;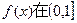 上的最大值.
上的最大值.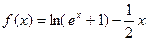 .
.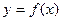 的单调区间,并判断函数的奇偶性;
的单调区间,并判断函数的奇偶性;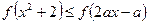 的解集是集合
的解集是集合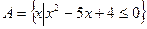 的子集,求实数
的子集,求实数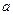 的取值范围.
的取值范围.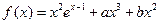 ,已知
,已知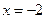 和
和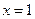 为
为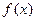 的极值点.
的极值点.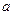 和
和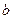 的值;
的值;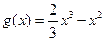 ,比较
,比较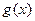 的大小.
的大小.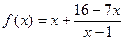 ,函数
,函数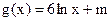 .
.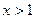 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;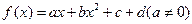 的导函数
的导函数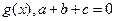 ,且
,且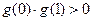 设
设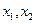 是方程
是方程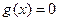 的两根,则|
的两根,则|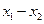 |的取值范围为
|的取值范围为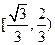 B
B 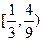 C
C 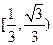 D
D