题目内容
已知函数f(x)=-x2+8x,g(x)=6lnx+m.(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;,若不存在,说明理由。
(Ⅰ) f(x)=2x(x-5)=2x2-10x(x∈R) (Ⅱ) 见解析
(I)∵f(x)是二次函数,且f(x)<0的解集是(0,5),∴可设f(x)=ax(x-5)(a>0),
∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
由已知,得6a=12,∴a=2,∴f(x)=2x(x-5)=2x2-10x(x∈R).
(II)方程f(x)+=0等价于方程2x3-10x2+37=0,
设h(x)=2x3-10x2+37,则h¢(x)=6x2-20x=2x(3x-10),
当x∈(0,)时,h¢(x)<0,h(x)是减函数;当x∈(,+∞)时,h¢(x)>0,h(x)是增函数,
∵h(3)=1>0,h()=-<0,h(4)=5>0,∴方程h(x)=0在区间(3,)、(,4)内分别有惟一实数根,而在(0,3),(4,+∞)内没有实数根,所以存在惟一的自然数m=3,使得方程f(x)+=0在区间(m,m+1)内有且只有两个不同的实数根.
∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
由已知,得6a=12,∴a=2,∴f(x)=2x(x-5)=2x2-10x(x∈R).
(II)方程f(x)+=0等价于方程2x3-10x2+37=0,
设h(x)=2x3-10x2+37,则h¢(x)=6x2-20x=2x(3x-10),
当x∈(0,)时,h¢(x)<0,h(x)是减函数;当x∈(,+∞)时,h¢(x)>0,h(x)是增函数,
∵h(3)=1>0,h()=-<0,h(4)=5>0,∴方程h(x)=0在区间(3,)、(,4)内分别有惟一实数根,而在(0,3),(4,+∞)内没有实数根,所以存在惟一的自然数m=3,使得方程f(x)+=0在区间(m,m+1)内有且只有两个不同的实数根.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
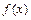 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,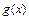 的图象与
的图象与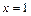 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时,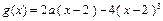 .
.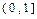 上为增函数,求
上为增函数,求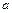 的取值范围;
的取值范围;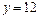 上?若存在,求出
上?若存在,求出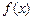 的定义域为
的定义域为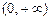 ,
,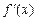 ,且对任意正数
,且对任意正数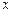 均有
均有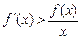 ,
,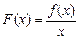 在
在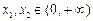 ,比较
,比较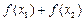 与
与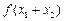 的大小,并证明你的结论;
的大小,并证明你的结论;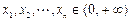 ,若
,若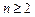 ,比较
,比较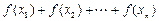 与
与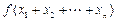 的大小,并证明你的结论.
的大小,并证明你的结论.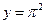 ,则
,则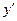 等于( )
等于( )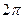
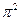
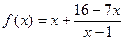 ,函数
,函数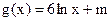 .
.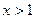 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;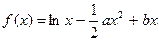
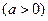 且
且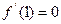 .
.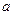 式子表示
式子表示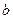 ;(Ⅱ)求
;(Ⅱ)求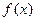 的单调区间;(Ⅲ)若
的单调区间;(Ⅲ)若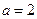 ,试求
,试求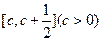 上的最大值.
上的最大值.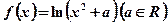 . (1)求在函数
. (1)求在函数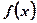 图像上点
图像上点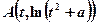 处的切线
处的切线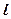 的方程;(2)若切线
的方程;(2)若切线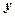 轴上的纵坐标截距记为
轴上的纵坐标截距记为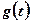 ,讨论
,讨论