题目内容
设向量 .
.
⑴若 ,求
,求 的值;
的值;
⑵设函数 ,求
,求 的最大值.
的最大值.
(1)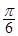 ;(2)
;(2)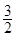 .
.
解析试题分析:(1)题中唯一已知条件是两个向量的模相等,那么我们把这个条件化简得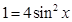 ,这样正好解出
,这样正好解出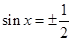 ,由三角函数值求角,还要确定角的范围,本题中
,由三角函数值求角,还要确定角的范围,本题中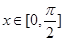 ,
,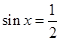 ,从而有
,从而有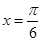 .
.
(2)同(1)把 化简,变为我们熟悉的函数,
化简,变为我们熟悉的函数,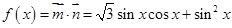 ,这是三角函数,一般要化为
,这是三角函数,一般要化为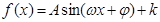 形式,然后利用正弦函数的性质解决问题,
形式,然后利用正弦函数的性质解决问题,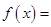
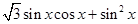
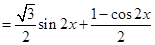
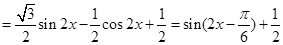 ,
,
因此 最大值为
最大值为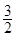 .
.
试题解析:(1)∵ ,∴
,∴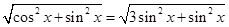 ,
,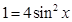 ,∵
,∵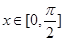 ,∴
,∴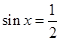 ,
,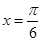 . 7分
. 7分
(2)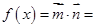
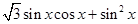
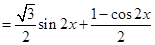
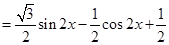
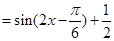
∵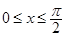 ∴
∴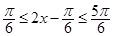
∴ 最大值为
最大值为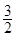 . 14分
. 14分
考点:(1)已知三角函数值,求角;(2)三角函数的最大值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的最大值为2,周期为
的最大值为2,周期为 .
. 的解析式,并由此求出函数的单调增区间;
的解析式,并由此求出函数的单调增区间;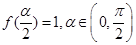 ,求
,求 的值.
的值.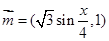 ,
, ,
,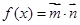
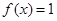 ,求
,求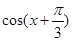 的值;
的值; 中,角
中,角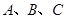 的对边分别是
的对边分别是 ,且满足
,且满足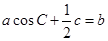 ,求函数
,求函数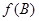 的取值范围.
的取值范围.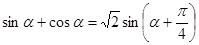
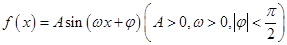 的部分图像如图所示.
的部分图像如图所示.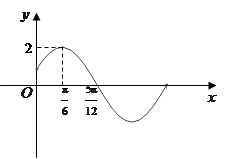
 的解析式;
的解析式;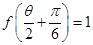 ,
,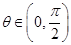 ,求
,求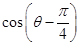 .
. 中,
中, 分别是内角
分别是内角 的对边,且
的对边,且
 ,若
,若
 的大小;
的大小; 为
为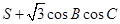 的最大值及此时
的最大值及此时 的值.
的值.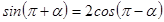 ,计算:
,计算: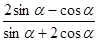 ;
; .
.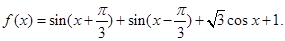
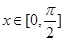 求
求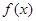 的值域;
的值域;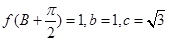 求
求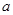 的值.
的值.
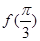 的值;
的值;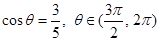 ,求
,求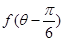 的值.
的值.