题目内容
某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元.该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3)求该商店月利润的最大值.(定义运算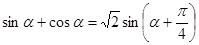
(1)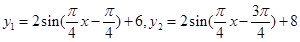 ;
;
(2)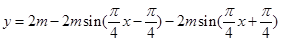
(3)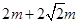
解析试题分析:(1)先设出函数解析式形如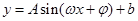 。函数最大值与最小值的差是2A;
。函数最大值与最小值的差是2A;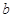 =函数最大值
=函数最大值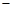 A或函数最小值+A;取最大值与最小值处的X值的差是半个周期,从而求出周期T,再利用周期公式
A或函数最小值+A;取最大值与最小值处的X值的差是半个周期,从而求出周期T,再利用周期公式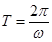 求出
求出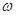 。最后代入点的坐标(或利用五点作图法)求
。最后代入点的坐标(或利用五点作图法)求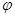 。具体过程见试题解析(2)月利润=一件的利润乘以件数即
。具体过程见试题解析(2)月利润=一件的利润乘以件数即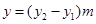 (3)化简变形为
(3)化简变形为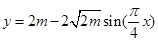 后根据三角函数的有界性求最值
后根据三角函数的有界性求最值
试题解析:设出厂价函数解析式为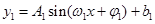
销售价格函数解析式为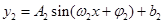 。
。
由题意得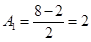 ;
;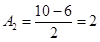 。
。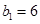 ;
;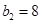 。
。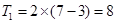 ;
;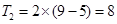
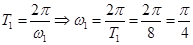 ;
;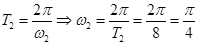 。
。
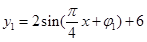 ;
;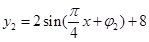
把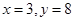 代入
代入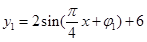 得,
得,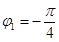
把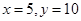 代入
代入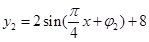 得,
得,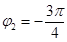
所以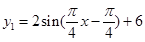 ;
;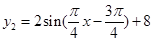 。
。
(2)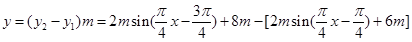
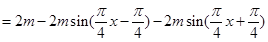
(3)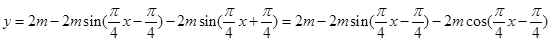
 ;所以当
;所以当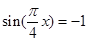 时,y取得最大值,最大值为
时,y取得最大值,最大值为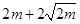
考点:三角函数解析式求法,三角函数最值问题

练习册系列答案
相关题目
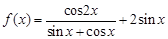 .
.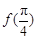 的值;
的值; 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.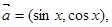
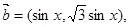
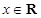 ,函数
,函数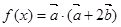 .
.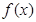 的单调递增区间;
的单调递增区间;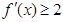 成立的
成立的 的取值集合.
的取值集合.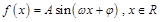 (其中
(其中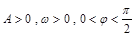 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为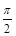 ,且图象上一个最低点为
,且图象上一个最低点为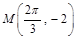 .
.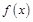 的解析式;
的解析式;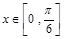 ,求
,求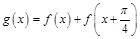 的值域.
的值域.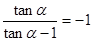 ,求下列各式的值:
,求下列各式的值: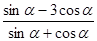 ;
;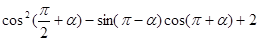 .
.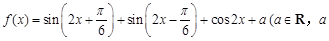 为常数).
为常数).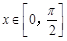 时,
时,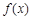 的最小值为
的最小值为 ,求a的值.
,求a的值. .
. ,求
,求 的值;
的值; ,求
,求 的最大值.
的最大值. ,求
,求 的集合.
的集合.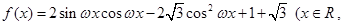
 >
> 的最小正周期是
的最小正周期是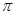 .
. <
< 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.