题目内容
7.在直角坐标系xOy中,O为坐标原点,已知点M的坐标为(3,2),若点N(x,y)的坐标满足$\left\{\begin{array}{l}{y≤x}\\{x+y≥2}\\{2x+y≥6}\end{array}\right.$,求$\overrightarrow{OM}$•$\overrightarrow{ON}$的最值.分析 化简可得$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+2y,从而转化为线性规划问题求最值即可.
解答 解:由题意,$\overrightarrow{OM}$=(3,2),$\overrightarrow{ON}$=(x,y);
故$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+2y=z,
作平面区域如下,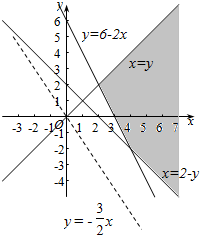 ,
,
3x+2y=z可化为y=-$\frac{3}{2}$x+$\frac{z}{2}$;
联立方程$\left\{\begin{array}{l}{y=6-2x}\\{x=2-y}\end{array}\right.$解得,
x=4,y=-2;
故结合图象可知,
在x=4,y=-2时,$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+2y有最小值3×4+2×(-2)=8;
没有最大值.
点评 本题考查了平面向量的数量积的应用及简单线性规划的问题,注意$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+2y看成目标函数即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知f(x)=ax3+bx+1(ab≠0),若f(2015)=k,则f(-2015)=( )
| A. | k-2 | B. | 2-k | C. | 1-k | D. | -k-1 |
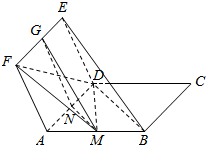 如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.