题目内容
【题目】已知![]() ,
,![]() 是函数
是函数![]() (其中常数
(其中常数![]() )图象上的两个动点,点
)图象上的两个动点,点![]() ,若
,若![]() 的最小值为0,则函数
的最小值为0,则函数![]() 的最大值为__________.
的最大值为__________.
【答案】![]()
【解析】
先推出f(x)的图象关于直线x=a对称,然后得出直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为
的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为![]() .
.
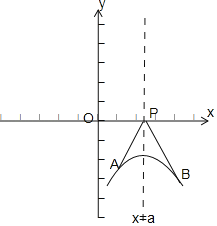
解:A,B是函数f(x)![]() (其中a>0)图象上的两个动点,
(其中a>0)图象上的两个动点,
当x<a时,f(x)=f(2a﹣x)=﹣e(2a﹣x)﹣2a=﹣e﹣x,
∴函数f(x)的图象关于直线x=a对称.
当点A,B分别位于分段函数的两支上,
且直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,
的最小值为0,
设PA与f(x)=﹣e﹣x相切于点A(x0,y0),
∴f′(x)=e﹣x,∴kAP=f′(x0)=e![]() ,解得x0=a﹣1,
,解得x0=a﹣1,
∵![]()
![]() 的最小值为0,∴
的最小值为0,∴![]() ⊥
⊥![]() ,
,
∴kPA=tan45°=1,∴e![]() 1,∴x0=0,
1,∴x0=0,
∴a=1,∴f(x)max![]() .
.
故答案为:![]()

练习册系列答案
相关题目
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元