题目内容
【题目】某农户计划种植莴笋和西红柿，种植面积不超过
亩，投入资金不超过
万元，假设种植莴笋和西红柿的产量、成本和售价如下表：
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么，该农户一年种植总利润（总利润=总销售收入-总种植成本）的最大值为____万元
【答案】
【解析】
设莴笋和西红柿的种植面积分别为
，
亩，种植总利润为z万元，然后根据题意建立关于x与y的约束条件，得到目标函数，利用线性规划的知识求出最值时的x和y的值即可．
设莴笋和西红柿的种植面积分别为，亩，一年的种植总利润为
万元.
由题意可得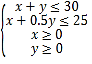
，
，
作出不等式组表示的可行域，如图所示，
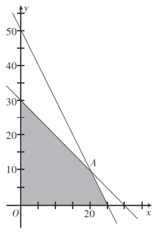
当直线
经过点
时，取得最大值，又
解得x=20，y=10,即
代入可得z=43，
故答案为.
【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
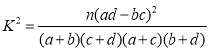
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
/p>
【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下图所示：
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 35 | 0.350 |
第3组 |
| 10 | 0.100 |
第4组 |
| 20 | 0.200 |
第5组 |
| 30 | 0.300 |
合计 | 100 | 1.00 | |
（1）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（2）在（1）的前提下，高校决定在这6名学生中，随机抽取2名学生接受A考官进行面试，求第4组至少有一名学生被A考官测试的概率.