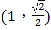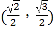题目内容
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面![]() 底面ABCD,且
底面ABCD,且![]() ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.
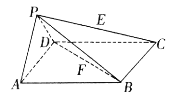
(I)求证:EF//平面PAD;
(II)求三棱锥F-DEC的体积;
(III)在线段CD上是否存在一点G,使得平面![]() 平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
【答案】(I)证明见解析;(II)![]() ;(Ⅲ)
;(Ⅲ) ![]() 的中点
的中点![]() 为满足条件的点
为满足条件的点
【解析】
(I)连接![]() 交
交![]() 于
于![]() ,利用三角形的中位线定理即可得到
,利用三角形的中位线定理即可得到![]() ,再利用线面平行的判定定理即可证明;
,再利用线面平行的判定定理即可证明;
(II)取![]() 的中点
的中点![]() ,连接
,连接![]() .由等腰三角形的性质可得
.由等腰三角形的性质可得![]() ,再利用面面垂直的性质可得
,再利用面面垂直的性质可得![]() 底面
底面![]() ,计算出三棱锥
,计算出三棱锥![]() 的高,利用三棱锥的体积计算公式即可得出;
的高,利用三棱锥的体积计算公式即可得出;
(III)易得![]() 的中点
的中点![]() 满足条件,再证明
满足条件,再证明![]()
![]() 平面
平面![]() 即可证明平面
即可证明平面![]() 平面PDC.
平面PDC.
(Ⅰ)证明:连接![]() ,则
,则![]() 是
是![]() 的中点,在
的中点,在![]() 中,
中, ![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;

(Ⅱ)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() ,∴
,∴![]() .
.
∵侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 底面
底面![]() .
.
∵![]() 为
为![]() 的中点,∴三棱锥
的中点,∴三棱锥![]() 的高为
的高为![]() ,
,
∵![]() ,且
,且![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴三棱锥![]() 的体积是
的体积是![]() .
.

(Ⅲ) ![]() 的中点
的中点![]() 为满足条件的点
为满足条件的点
证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
则因为E,F分别为PC,BD的中点,![]() 为
为![]() 的中点,故
的中点,故![]() 为
为![]() 的中位线,
的中位线,
故![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .因为
.因为![]() ,故平面
,故平面![]() 平面
平面![]() .
.
又正方形![]() ,故
,故![]() ,
,
又侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,故平面
,故平面![]() 平面PDC
平面PDC
故![]() 的中点
的中点![]() 为满足条件的点.
为满足条件的点.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目