题目内容
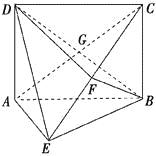
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)证明 ∵AD⊥平面ABE,AD∥BC, ∴BC⊥平面ABE,则AE⊥BC.
又∵BF⊥平面ACE,则AE⊥BF,
又BC∩BF=B,∴AE⊥平面BCE.
(2)证明 由题意可得G是AC的中点,连结FG,
∵BF⊥平面ACE,∴CE⊥BF.
而BC=BE,∴F是EC的中点,
在△AEC中,FG∥AE,∴AE∥平面BFD.
(3)∵AE∥FG.
而AE⊥平面BCE,
∴FG⊥平面BCF.
∵G是AC中点,F是CE中点,
∴FG∥AE且FG=![]() AE=1.
AE=1.
∴Rt△BCE中,BF=CE=CF=![]() ,
,
∴S△CFB=![]() ×
×![]() ×
×![]() =1.
=1.
∴VC-BGF=VG-BCF=·S△CFB·FG=![]() .
.

练习册系列答案
相关题目