题目内容
【题目】下列说法正确的是( )
A. 命题![]() ,
,![]() 都是假命题,则命题“
都是假命题,则命题“![]() ”为真命题.
”为真命题.
B. ![]() ,函数
,函数![]() 都不是奇函数.
都不是奇函数.
C. 函数![]() 的图像关于
的图像关于![]() 对称 .
对称 .
D. 将函数![]() 的图像上所有点的横坐标伸长到原来的2倍后得到
的图像上所有点的横坐标伸长到原来的2倍后得到![]()
【答案】C
【解析】
运用复合命题的真假可判断A;可取φ![]() ,结合诱导公式和奇函数的定义可判断B,由f(
,结合诱导公式和奇函数的定义可判断B,由f(![]() )=1,可判断C;运用图象变换可判断D.
)=1,可判断C;运用图象变换可判断D.
对于A,命题p,q都是假命题,可得¬p为真,则命题“¬p∧q”为假命题,故A错误;
对于B,当φ![]() 时,f(x)=sin(2x
时,f(x)=sin(2x![]() ),即f(x)=-sin(2x)为奇函数,故B错误.
),即f(x)=-sin(2x)为奇函数,故B错误.
对于C,函数f(x)=sin(2x![]() ),由f(
),由f(![]() )=sin(
)=sin(![]() )=1,且为f(x)的最大值,
)=1,且为f(x)的最大值,
可得f(x)的图象关于x![]() 对称,故C正确;
对称,故C正确;
对于D,将函数y=sin2x的图象上所有点的横坐标伸长到原来的2倍后得到y=sinx,故D错误;
故选:C.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与![]() 的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与![]() 的浓度的数据如下表:
的浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 100 | 102 | 108 | 114 | 116 |
| 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若周六同一时间段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时![]() 的浓度为多少.
的浓度为多少.
参考公式: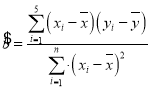 ,
,![]() .
.