题目内容
【题目】甲、乙两名射击运动员一次射击命中目标的概率分别是0.7,0.6,且每次射击命中与否相互之间没有影响,求:
(1)甲射击三次,第三次才命中目标的概率;
(2)甲、乙两人在第一次射击中至少有一人命中目标的概率;
(3)甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率.
【答案】(1)![]() ;(2)0.88;(3)
;(2)0.88;(3)![]() .
.
【解析】
(1)“甲第三次才命中目标”为事件![]() ,且三次射击相互独立,利用独立重复试验概率计算公式即可求得答案;
,且三次射击相互独立,利用独立重复试验概率计算公式即可求得答案;
(2)求该事件的反面的概率,用1减其即可;
(3)设“甲在两次射击命中目标i次”为事件![]() ,“乙在两次射击命中目标i次”为事件
,“乙在两次射击命中目标i次”为事件![]() ,则事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为
,则事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为![]() ,用独立重复试验概率计算公式即可求得答案.
,用独立重复试验概率计算公式即可求得答案.
记“甲第i次射击命中目标”为事件![]() ,“乙第i次射击命中目标”为事件
,“乙第i次射击命中目标”为事件![]() ,依题意得
,依题意得![]() ,
,![]() ,且
,且![]() ,
,![]() (
(![]() )相互独立.
)相互独立.
(1)“甲第三次才命中目标”为事件![]() ,且三次射击相互独立,
,且三次射击相互独立,
![]() .
.
答:甲第三次才命中目标的概率为![]() .
.
(2)“甲、乙两人在第一次射击中至少有一人命中目标”为事件C.
![]() .
.
答:甲、乙两人在第一次射击中至少有一人命中目标的概率为0.88.
(3)设“甲在两次射击命中目标i次”为事件![]() ,
,
“乙在两次射击命中目标i次”为事件![]() ,
,
![]() 事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为
事件“甲、乙各射击两次,甲比乙命中目标次数恰好多一次”可表示为![]() ,且
,且![]() ,
,![]() 为互斥事件,
为互斥事件,
![]() 所求的概率为
所求的概率为![]()
![]()
![]()
答:甲、乙各射击两次,甲比乙命中目标的次数恰好多一次的概率为![]() .
.

 口算能手系列答案
口算能手系列答案【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与![]() 的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与![]() 的浓度的数据如下表:
的浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 100 | 102 | 108 | 114 | 116 |
| 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若周六同一时间段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时![]() 的浓度为多少.
的浓度为多少.
参考公式: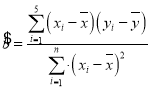 ,
,![]() .
.