题目内容
【题目】若![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() ,
,![]() 为一素数,
为一素数,![]() 、
、![]() 、
、![]() 的
的![]() 进制表示分别为
进制表示分别为![]() ,其中,
,其中,![]() .证明:
.证明:
(1)若![]() ,且对整数
,且对整数![]()
![]() 均有
均有![]() ,则
,则![]() ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
(2)![]()
![]() ,其中,
,其中,![]() 表示集合A中元素的个数.
表示集合A中元素的个数.
【答案】(1)见解析(2)见解析
【解析】
(1)注意到,![]() .
.
于是,![]() .
.
则![]() .
.
故![]() .
.
(1)若![]() ,且
,且![]() ,则记
,则记![]() .
.
以![]() ,
,![]() 为例,易得
为例,易得![]() .
.
一般地,关于![]() 不难得出公式:
不难得出公式: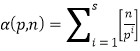 .
.
由(1)得![]() .
.
令![]() .则
.则![]() .
.
先介绍两个引理.
引理1 ![]() ,其中,
,其中,![]() .
.
引理1的证明 事实上,由![]() ,
,
知![]() .
.
引理2 若存在整数![]() ,有
,有![]() ,
,
而![]() ,则存在整数
,则存在整数![]()
![]() ,有
,有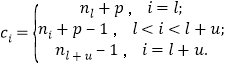
引理2的证明 由![]() ,即
,即![]() .
.
又由![]() ,得
,得![]()
![]() .
.
于是,![]() .
.
因为![]() ,所以,
,所以,![]() .
.
故![]() .
.
从而,![]() .
.
若![]() ,则
,则![]() ,即
,即![]() .
.
若![]() ,则
,则![]() .
.
由![]() ,
,
知![]() .
.
于是,![]() .
.
所以,![]() ,即
,即![]() .
.
否则,![]()
由于![]() ,从而,一定存在整数
,从而,一定存在整数![]() 使得
使得![]() ,即
,即![]() .
.
回到原题.
相对于![]() 的
的![]() 进制表示,称
进制表示,称![]() 中的一段
中的一段![]() 是长度为
是长度为![]() 的一个“下移端”,记为
的一个“下移端”,记为![]() .
.
显然,![]() .
.
从而,![]() ,即为引理2的条件.
,即为引理2的条件.
因此,当![]() 时,若
时,若![]() ,则
,则![]() ,存在另一个下移段.
,存在另一个下移段.
由上述讨论,知若![]() 中有
中有![]() 个
个![]() ,则
,则![]() 中存在
中存在![]() 个下移段
个下移段![]()
![]() .
.
当![]() 时,显然,
时,显然,![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ,仍有
,仍有![]() .
.
上述两种情形均有![]() .
.
由引理1及(1)知![]() .
.
对任意的![]() ,当
,当![]() 时,由引理1知
时,由引理1知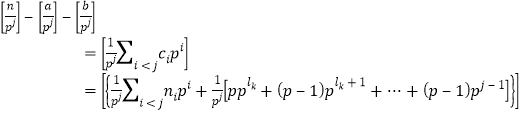
![]() .
.
综上,即得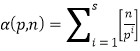
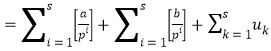 .
.
令![]() .则
.则![]() .
.
故![]()
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的女学生中随机选出100名并统计她们的身高(单位:cm),得到的频数分布表如下:
分组 |
|
|
|
|
频数 | 20 | 20 | 50 | 10 |
(1)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 内的女生应抽取几人?
内的女生应抽取几人?
(2)在(1)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
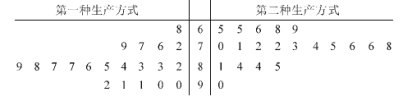
(1)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: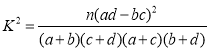
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |