题目内容
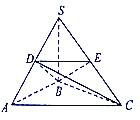
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的大小.
的平面角的大小.
【答案】(Ⅰ)证明过程详见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)已知SB、AB、BC两两互相垂直,故可建立空间直角坐标系如下图.根据线段长度可求出相应点的坐标,从而可推出![]() ,则
,则![]() ,所以平面
,所以平面![]() 平面BCD.
平面BCD.
(Ⅱ)求出两个平面的法向量,利用法向量夹角与二面角平面角的关系求出平面角的大小.
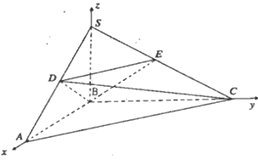
(Ⅰ)![]() .
.
又因![]() ,所以建立如上图所示的坐标系.
,所以建立如上图所示的坐标系.
所以A(2,0,0),![]() ,
,![]() ,
,
D(1,0,1),![]() ,S(0,0,2)
,S(0,0,2)
易得,![]() ,
,![]() ,
,![]()
又![]() ,
,![]()
又![]()
又因![]() ,
,
所以平面![]() 平面BCD.
平面BCD.
(Ⅱ)又![]()
设平面BDE的法向量为![]() ,
,
则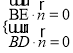 ,即
,即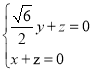
所以![]()
又因平面SBD的法向量为![]()
所以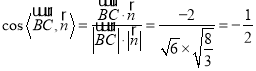
由图可得二面角为锐角,所以二面角![]() 的平面角的大小为
的平面角的大小为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的女学生中随机选出100名并统计她们的身高(单位:cm),得到的频数分布表如下:
分组 |
|
|
|
|
频数 | 20 | 20 | 50 | 10 |
(1)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 内的女生应抽取几人?
内的女生应抽取几人?
(2)在(1)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.