��Ŀ����
����Ŀ��ij��λ��Ҫ�Ӽס���![]() ����ѡ��һ�˲μ��¸�λ��ѵ���ر���֯��
����ѡ��һ�˲μ��¸�λ��ѵ���ر���֯��![]() ��ר��Ŀ��ԣ��ɼ�ͳ�����£�
��ר��Ŀ��ԣ��ɼ�ͳ�����£�
��һ�� | �ڶ��� | ������ | ������ | ������ | |
�ijɼ� |
|
|
|
|
|
�ҵijɼ� |
|
|
|
|
|
��1�������й�ͳ��֪ʶ���ش�����:���Ӽס���![]() ����ѡ��
����ѡ��![]() �˲μ��¸���ѵ������Ϊѡ˭���ʣ���˵�����ɣ�
�˲μ��¸���ѵ������Ϊѡ˭���ʣ���˵�����ɣ�
��2�������йؘ���֪ʶ������������⣺
�Ӽס���![]() �˵ijɼ��и������ȡһ������鵽�ijɼ�Ϊ
�˵ijɼ��и������ȡһ������鵽�ijɼ�Ϊ![]() ���鵽�ҵijɼ�Ϊ
���鵽�ҵijɼ�Ϊ![]() ����
����![]() ��ʾ��������
��ʾ��������![]() ���¼������¼�
���¼������¼�![]() �ĸ���.
�ĸ���.
���𰸡�(1) �ɼ��ʺϣ�(2) ![]()
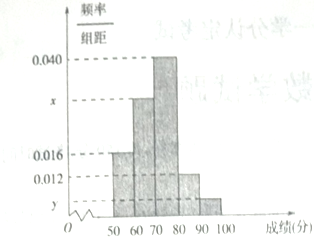
�������������������1���������߳ɼ���ƽ�����ͷ��ƽ������ȣ���ѡ���С�ıȽ��ȶ�.��2�������оٷ��г����еĿ�������![]() �֣����з����������
�֣����з����������![]() �֣��ɴ���ø���Ϊ
�֣��ɴ���ø���Ϊ![]() .
.
���������
(1)��ƽ���ɼ�Ϊ![]() ���ҵ�ƽ���ɼ�Ϊ
���ҵ�ƽ���ɼ�Ϊ![]() ���ʼ��Ҷ��˵�ƽ��ˮƽһ��. �ijɼ�����
���ʼ��Ҷ��˵�ƽ��ˮƽһ��. �ijɼ�����![]() ���ҵijɼ�����
���ҵijɼ�����![]() ��
�� ![]() ����Ӧ�ɼ��ʺ�.
����Ӧ�ɼ��ʺ�.
(2)�Ӽ��Ҷ��˵ijɼ��и������һ������׳鵽�ijɼ�Ϊ![]() ���ҳ鵽�ijɼ�Ϊ
���ҳ鵽�ijɼ�Ϊ![]() �������е�
�������е�![]() ��
��![]()
![]()
![]()
![]()
![]() ��
��![]() ����������������
����������������![]() ����
���� ![]() ����
����![]() ���������¼��ĸ���Ϊ
���������¼��ĸ���Ϊ![]() .
.

����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ��ǧԪ����������
����λ��ǧԪ����������![]() ����λ����Ԫ����Ӱ�죬�Խ�5���������
����λ����Ԫ����Ӱ�죬�Խ�5���������![]() ��������
��������![]() ��
��![]() ��������ͳ�ƣ��г����±���
��������ͳ�ƣ��г����±���
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
Ա��С����С��ֱ��ṩ�˲�ͬ�ķ�����
��1��С���������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ�������������
�Ĺ�ϵ�������������![]() ����
����![]() �����Իع鷽������ϵ����ȷ��0.01��
�����Իع鷽������ϵ����ȷ��0.01��
��2��С�����ѡ������ع�ģ�����![]() ��
��![]() �Ĺ�ϵ���õ��˻ع鷽����
�Ĺ�ϵ���õ��˻ع鷽����![]() �����ṩ�����ָ��
�����ṩ�����ָ��![]() ���������ָ��˵��ѡ���ĸ�ģ�����ʣ���Ԥ����������Ϊ4��Ԫ����������ȷ��0.01����С��Ҳ�ṩ�����ķ�����������
���������ָ��˵��ѡ���ĸ�ģ�����ʣ���Ԥ����������Ϊ4��Ԫ����������ȷ��0.01����С��Ҳ�ṩ�����ķ�����������![]() ��
��
�ο���ʽ�����ָ��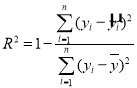
�ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
 ��
��![]() ���������
���������![]() ��
��![]() ��
��