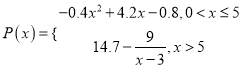题目内容
【题目】定义在![]() 上的单调递减函数
上的单调递减函数![]() ,对任意
,对任意![]() 都有
都有![]() ,
, ![]() .
.
(Ⅰ)判断函数![]() 的奇偶性,并证明之;
的奇偶性,并证明之;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() (
(![]() 为常实数)都成立,求
为常实数)都成立,求![]() 的取值范围;(Ⅲ)设
的取值范围;(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
若![]()
![]()
![]() ,
, ![]() ,比较
,比较![]() 的大小并说明理由.
的大小并说明理由.
【答案】(Ⅰ)![]() 为
为![]() 上的奇函数;证明见解析(Ⅱ)
上的奇函数;证明见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]() ;
;
【解析】【试题分析】(Ⅰ)先取取![]() 得
得![]() ,再取
,再取![]() 得
得![]()
,进而可得对任意![]() 都有
都有![]() ,运用定义可证
,运用定义可证![]() 为
为![]() 上奇函数;(Ⅱ)先借助函数的奇偶性、单调性将不等式
上奇函数;(Ⅱ)先借助函数的奇偶性、单调性将不等式![]() 进行等价转化为
进行等价转化为![]() ,再将不等式中的参数
,再将不等式中的参数![]() 分离出来,将该不等式化为“
分离出来,将该不等式化为“![]() 在
在![]() 上恒成立”问题,最后通过求函数
上恒成立”问题,最后通过求函数![]()
的值域即可;(Ⅲ)先依据题设条件将![]() 的解析式化简求出,再进行分析比较其大小:
的解析式化简求出,再进行分析比较其大小:
(Ⅰ)解: ![]() 为
为![]() 上的奇函数
上的奇函数
证明:取![]() 得
得![]()
∴![]()
取![]() 得
得![]()
即:对任意![]() 都有
都有![]()
∴![]()
∴![]() 为
为![]() 上奇函数
上奇函数
(Ⅱ)∵![]()
∴![]()
∵![]() 在
在![]() 上单减
上单减
∴![]() 在
在![]() 上恒成立
上恒成立
∴![]()
∴![]() 在
在![]() 上恒成立
上恒成立
![]() 在
在![]() 上恒成立
上恒成立
![]()
![]()
∴当![]() 时,
时, ![]()
∴![]()
即![]()
(Ⅲ)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]() 在
在![]() 单增,在
单增,在![]() 上单减
上单减
![]()
![]()
![]()
![]()
![]()
![]()
![]()
同理:
![]()
![]()
![]()
![]()
![]()
![]()
∴![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为![]() ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为![]() ,现从
,现从![]() ,
, ![]() 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.