题目内容
15.函数f(x)=${log_{\frac{1}{2}}}$x-x+4的零点位于区间( )| A. | $(\frac{1}{2},1)$ | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 可判断函数f(x)=${log_{\frac{1}{2}}}$x-x+4在(0,+∞)上减函数,结合函数零点的判定定理判断零点所在的区间即可.
解答 解:函数f(x)=${log_{\frac{1}{2}}}$x-x+4在(0,+∞)上减函数,
f(2)=${log_{\frac{1}{2}}}$2-2+4=1>0,f(3)=${log_{\frac{1}{2}}}$3-3+4=${log_{\frac{1}{2}}}$3+1<0;
故f(2)f(3)<0,
故函数f(x)=${log_{\frac{1}{2}}}$x-x+4的零点在(2,3)之间,
故选:C.
点评 本题考查了对数函数的应用及函数零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
20.若a,b,c∈(0,+∞),且a+b+c=1,则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\root{3}{2}}{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{1}{9}$ |
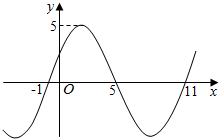 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.