题目内容
18.将函数f(x)=2sin(2x+φ)的图象向右平移$\frac{π}{6}$个单位后,得到的函数图象关于y轴对称,则φ的最小正值为$\frac{5π}{6}$.分析 利用函数图象的平移得到平移后的图象的解析式,再根据图象关于y轴对称可知平移后的函数为偶函数,即函数y=2sin(2x-$\frac{π}{3}$+φ)为偶函数,由此可得-$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z.即可求出φ的最小正值.
解答 解:把函数y=2sin(2x+φ)的图象沿x轴向右平移$\frac{π}{6}$个单位后,得到图象的函数解析式为:
y=2sin[2(x-$\frac{π}{6}$)+φ]=2sin(2x-$\frac{π}{3}$+φ).
∵得到的图象关于y轴对称,
∴函数y=2sin(2x-$\frac{π}{3}$+φ)为偶函数.
则-$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z.
即φ=kπ+$\frac{5π}{6}$,k∈Z.
取k=0时,得φ的最小正值为$\frac{5π}{6}$.
故答案为:$\frac{5π}{6}$.
点评 本题考查y=Asin(ωx+φ)的图象变换,考查了三角函数中诱导公式的应用,关键是明确函数的奇偶性与图象之间的关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
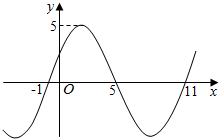 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.