题目内容
1.在直角坐标系xOy中,圆C的参数方程为$\left\{{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}}\right.$(θ为参数).已知A(-2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值.分析 圆C的参数方程为$\left\{{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}}\right.$(θ为参数),化为普通方程,利用M(x,y)到直线AB:x-y+2=0的距离,表示△ABM的面积,通过三角函数的最值,求解△ABM面积的最大值.
解答 选修4-4:坐标系与参数方程
解:圆C的参数方程为$\left\{{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}}\right.$(θ为参数),∴普通方程为(x-3)2+(y+4)2=4,点M(x,y)到直线AB:x-y+2=0的距离为$d=\frac{|2cosθ-2sinθ+9|}{{\sqrt{2}}}$,△ABM的面积$S=\frac{1}{2}×|AB|×d=|2cosθ-2sinθ+9|$=$|2\sqrt{2}sin(\frac{π}{4}-θ)+9|$,∴△ABM面积的最大值为$9+2\sqrt{2}$.
点评 本题考查参数方程与普通方程的互化,点到直线的距离以及三角函数的最值的应用,考查转化思想以及计算能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
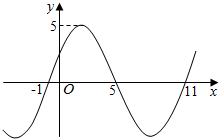 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.