题目内容
14.设非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,且$|\begin{array}{l}{\overrightarrow{a}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{b}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{c}}\\{\;}\end{array}|$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 把已知式子平方由数量积的运算易得向量夹角的余弦值,可得夹角.
解答 解:由题意可得${\overrightarrow{c}}^{2}$=($\overrightarrow{a}$+$\overrightarrow{b}$)2,
∴|$\overrightarrow{c}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ,其中θ为向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角,
∵$|\begin{array}{l}{\overrightarrow{a}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{b}}\\{\;}\end{array}|$=$|\begin{array}{l}{\overrightarrow{c}}\\{\;}\end{array}|$,∴cosθ=-$\frac{1}{2}$,
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$
故选:D
点评 本题考查平面向量的夹角,属基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
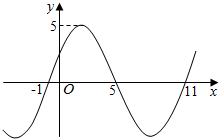 函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)在R上的部分图象如图所示,则ω的值为$\frac{π}{6}$.