题目内容
(1)设x≥1,y≥1,证明x+y+ ≤
≤ +
+ +xy;
+xy;
(2)1<a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.
 ≤
≤ +
+ +xy;
+xy;(2)1<a≤b≤c,证明logab+logbc+logca≤logba+logcb+logac.
(1)见解析(2)见解析
(1)由于x≥1,y≥1,
要证x+y+ ≤
≤ +
+ +xy,
+xy,
只需证xy(x+y)+1≤y+x+(xy)2.
因为[y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1).
由条件x≥1,y≥1,得(xy-1)(x-1)(y-1)≥0,
从而所要证明的不等式成立.
(2)设logab=x,logbc=y,由对数的换底公式得logca= ,logba=
,logba= ,logcb=
,logcb= ,logac=xy.
,logac=xy.
于是,所要证明的不等式即为x+y+ ≤
≤ +
+ +xy.
+xy.
其中x=logab≥1,y=logbc≥1.
故由(1)可知所要证明的不等式成立.
要证x+y+
 ≤
≤ +
+ +xy,
+xy,只需证xy(x+y)+1≤y+x+(xy)2.
因为[y+x+(xy)2]-[xy(x+y)+1]
=[(xy)2-1]-[xy(x+y)-(x+y)]
=(xy+1)(xy-1)-(x+y)(xy-1)
=(xy-1)(xy-x-y+1)
=(xy-1)(x-1)(y-1).
由条件x≥1,y≥1,得(xy-1)(x-1)(y-1)≥0,
从而所要证明的不等式成立.
(2)设logab=x,logbc=y,由对数的换底公式得logca=
 ,logba=
,logba= ,logcb=
,logcb= ,logac=xy.
,logac=xy.于是,所要证明的不等式即为x+y+
 ≤
≤ +
+ +xy.
+xy.其中x=logab≥1,y=logbc≥1.
故由(1)可知所要证明的不等式成立.

练习册系列答案
相关题目
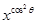 ·
·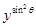 ,则a与b的大小关系是 .
,则a与b的大小关系是 . (x>-1)的值域.
(x>-1)的值域. ,
, ,
, ( )
( )