题目内容
已知命题“?x∈R，|x－a|＋|x＋1|≤2”是假命题，则实数a的取值范围是________．
(－∞，－3)∪(1，＋∞)
依题意知，对任意x∈R，都有|x－a|＋|x＋1|＞2；由于|x－a|＋|x＋1|≥|(x－a)－(x＋1)|＝|a＋1|，
因此有|a＋1|＞2，a＋1＜－2或a＋1＞2，即a＜－3或a＞1.
所以实数a的取值范围是(－∞，－3)∪(1，＋∞)．
因此有|a＋1|＞2，a＋1＜－2或a＋1＞2，即a＜－3或a＞1.
所以实数a的取值范围是(－∞，－3)∪(1，＋∞)．
练习册系列答案
相关题目
；
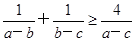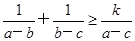恒成立的k的最大值．
,n∈N*,试比较f(
)与
的大小,并且说明理由.
≤
＋
＋xy；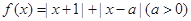
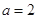时，解不等式
；
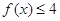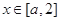恒成立，求实数
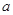的取值范围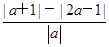
对任意实数a≠0恒成立，则x的取值集合是________．
+b
>a
>
,则实数m的取值范围是( )