题目内容
已知对于任意非零实数m,不等式|2m-1|+|1-m|≥|m|(|x-1|-|2x+3|)恒成立,则实数x的取值范围为____________.
(-∞,-3]∪[-1,+∞)
由题意只要求|x-1|-|2x+3|≤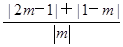 恒成立时实数x的取值范围.
恒成立时实数x的取值范围.
∵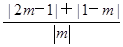 ≥
≥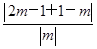 =1.
=1.
∴只需|x-1|-|2x+3|≤1.
①当x≤-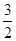 时,原式等价于1-x+2x+3≤1,
时,原式等价于1-x+2x+3≤1,
即x≤-3,∴x≤-3.
②当-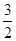 <x<1时,原式等价于1-x-2x-3≤1,
<x<1时,原式等价于1-x-2x-3≤1,
即x≥-1,∴-1≤x<1.
③当x≥1时,原式等价于x-1-2x-3≤1,
即x≥-5,∴x≥1.
综上x的取值范围为(-∞,-3]∪[-1,+∞).
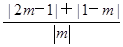 恒成立时实数x的取值范围.
恒成立时实数x的取值范围.∵
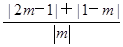 ≥
≥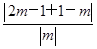 =1.
=1.∴只需|x-1|-|2x+3|≤1.
①当x≤-
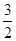 时,原式等价于1-x+2x+3≤1,
时,原式等价于1-x+2x+3≤1,即x≤-3,∴x≤-3.
②当-
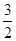 <x<1时,原式等价于1-x-2x-3≤1,
<x<1时,原式等价于1-x-2x-3≤1,即x≥-1,∴-1≤x<1.
③当x≥1时,原式等价于x-1-2x-3≤1,
即x≥-5,∴x≥1.
综上x的取值范围为(-∞,-3]∪[-1,+∞).

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,n∈N*,试比较f(
,n∈N*,试比较f( )与
)与 的大小,并且说明理由.
的大小,并且说明理由. ≤
≤ +
+ +xy;
+xy; 则以下不等式中不恒成立的是( )
则以下不等式中不恒成立的是( )
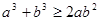


 >0”成立的( )
>0”成立的( )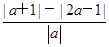 对任意实数a≠0恒成立,则x的取值集合是________.
对任意实数a≠0恒成立,则x的取值集合是________.

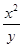 ≤9,则
≤9,则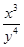 的最大值是________.
的最大值是________.