题目内容
【题目】已知![]() 的三个顶点落在半径为
的三个顶点落在半径为![]() 的球
的球![]() 的表面上,三角形有一个角为
的表面上,三角形有一个角为![]() 且其对边长为3,球心
且其对边长为3,球心![]() 到
到![]() 所在的平面的距离恰好等于半径
所在的平面的距离恰好等于半径![]() 的一半,点
的一半,点![]() 为球面上任意一点,则
为球面上任意一点,则![]() 三棱锥的体积的最大值为( )
三棱锥的体积的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设![]() 外接圆的圆心为
外接圆的圆心为![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,设
,设![]() 外接圆的半径为
外接圆的半径为![]() ,
,![]() ,利用正弦定理即可求得:
,利用正弦定理即可求得:![]() ,再利用截面圆的性质可列方程:
,再利用截面圆的性质可列方程:![]() ,即可求得
,即可求得![]() ,即可求得点
,即可求得点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为![]() ,利用余弦定理及基本不等式即可求得:
,利用余弦定理及基本不等式即可求得:![]() ,再利用锥体体积公式计算即可得解。
,再利用锥体体积公式计算即可得解。
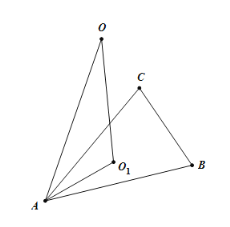
设![]() 外接圆的圆心为
外接圆的圆心为![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]()
设![]() 外接圆的半径为
外接圆的半径为![]() ,
,![]() ,
,![]()
由正弦定理可得: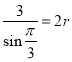 ,解得:
,解得:![]()
由球的截面圆性质可得:![]() ,解得:
,解得:![]()
所以点![]() 到平面
到平面![]() 的距离的最大值为:
的距离的最大值为:![]() .
.
在![]() 中,由余弦定理可得:
中,由余弦定理可得:![]()
当且仅当![]() 时,等号成立,所以
时,等号成立,所以![]() .
.
所以![]() ,当且仅当
,当且仅当![]() 时,等号成立.
时,等号成立.
当三棱锥![]() 的底面面积最大,高最大时,其体积最大.
的底面面积最大,高最大时,其体积最大.
所以三棱锥![]() 的体积的最大值为
的体积的最大值为![]()
故选:C

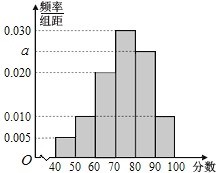
【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历的三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

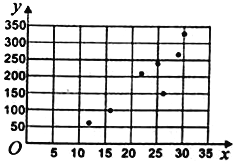
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为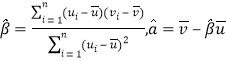 .
.
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.