题目内容
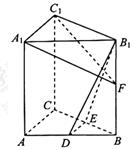
【题目】已知
的三个顶点落在半径为
的球
的表面上，三角形有一个角为
且其对边长为3，球心到所在的平面的距离恰好等于半径的一半，点
为球面上任意一点，则
三棱锥的体积的最大值为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
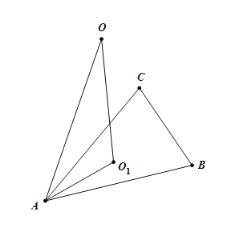
设
外接圆的圆心为
，则
平面
，所以
，设外接圆的半径为
，
，利用正弦定理即可求得：
，再利用截面圆的性质可列方程：
，即可求得
，即可求得点
到平面的距离的最大值为
，利用余弦定理及基本不等式即可求得：
，再利用锥体体积公式计算即可得解。
设外接圆的圆心为，则平面，所以
设外接圆的半径为，，
由正弦定理可得：
，解得：
由球的截面圆性质可得：
，解得：
所以点到平面的距离的最大值为：
.
在中，由余弦定理可得：
当且仅当
时，等号成立，所以.
所以
，当且仅当时，等号成立.
当三棱锥
的底面面积最大，高最大时，其体积最大.
所以三棱锥的体积的最大值为
故选：C
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
