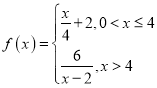题目内容
【题目】数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,证明
,证明![]() 是等差数列;
是等差数列;
(2)求![]() 的通项公式.
的通项公式.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即可证得;
(2)由(1)得bn=1+2(n-1)=2n-1,即an+1-an=2n-1,进而利用累加求通项公式即可.
试题解析:
(1)证明 由an+2=2an+1-an+2,得an+2-an+1=an+1-an+2,即bn+1=bn+2.
又b1=a2-a1=1,所以{bn}是首项为1,公差为2的等差数列.
(2)解 由(1)得bn=1+2(n-1)=2n-1,即an+1-an=2n-1.
于是![]() (ak+1-ak)=
(ak+1-ak)=![]() (2k-1),所以an+1-a1=n2,即an+1=n2+a1.
(2k-1),所以an+1-a1=n2,即an+1=n2+a1.
又a1=1,所以an=n2-2n+2,经检验,此式对n=1亦成立,
所以,{an}的通项公式为an=n2-2n+2.

练习册系列答案
相关题目