题目内容
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
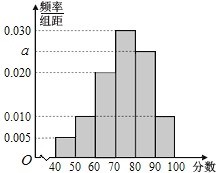
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)利用频率分布直方图小长方形的面积之和是1可得;
(Ⅱ)由题意利用频率近似概率可得;
(Ⅲ)由题意填写列联表,计算观测值,对照临界值得出结论.
(Ⅰ)由题可得![]() ,
,
解得![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,
则比赛成绩不低于![]() 分的频率为
分的频率为![]() ,
,
故从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分的概率约为
分的概率约为![]() .
.
(Ⅲ)由(Ⅱ)知,在抽取的![]() 名学生中,比赛成绩优秀的有
名学生中,比赛成绩优秀的有![]() 人,
人,
由此可得完整的![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
所以![]() 的观测值
的观测值![]() ,
,
所以没有![]() 的把握认为“比赛成绩是否优秀与性别有关”.
的把握认为“比赛成绩是否优秀与性别有关”.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
【题目】针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的女生人数是男生人数的![]() ,男生喜欢抖音的人数占男生人数的
,男生喜欢抖音的人数占男生人数的![]() ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数![]() 若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
若有95%的把握认为是否喜欢抖音和性别有关,则男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
