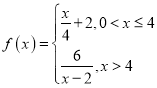题目内容
【题目】设函数![]() ,下列四个命题中真命题的序号是( )
,下列四个命题中真命题的序号是( )
(1)![]() 是偶函数;(2)当且仅当
是偶函数;(2)当且仅当![]() 时,
时,![]() 有最小值;
有最小值;
(3)![]() 在
在![]() 上是增函数;(4)方程
上是增函数;(4)方程![]() 有无数个实根.
有无数个实根.
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
【答案】A
【解析】
由![]() 可判断(1);根据绝对值的几何意义可得
可判断(1);根据绝对值的几何意义可得![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)![]()
![]() (当且仅当
(当且仅当![]() 时取等号),可判断(2);在
时取等号),可判断(2);在![]() 内有
内有![]() ,可判断(3);根据函数
,可判断(3);根据函数![]() 为偶函数,且
为偶函数,且![]() 时,
时,![]() ,所以要使
,所以要使![]() 成立,需
成立,需![]() 或
或![]() ,或
,或 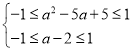 ,解得
,解得![]() 可判断(4).
可判断(4).
由![]() 得
得
![]()
![]() ,
,
所以![]() 为偶函数,故(1)正确;
为偶函数,故(1)正确;
根据绝对值的几何意义可得![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)![]()
![]() (当且仅当
(当且仅当![]() 时取等号),所以
时取等号),所以
![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时取等号,所以(2)不正确;
时取等号,所以(2)不正确;
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
所以![]() ,所以(3)不正确;
,所以(3)不正确;
因为函数![]() 为偶函数,且
为偶函数,且![]() 时,
时,![]() ,
,
所以使![]() 成立,需
成立,需![]() 或
或![]() ,或
,或 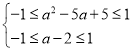 ,
,
解得![]() 无解或
无解或![]() 或
或![]() 或
或![]()
所以![]() 或
或![]() ,
,
所以方程![]() 有无数个实根,所以(4)正确;
有无数个实根,所以(4)正确;
所以正确命题的序号是(1)(4),
故选:A.

练习册系列答案
相关题目