题目内容
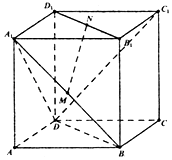
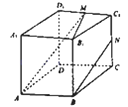
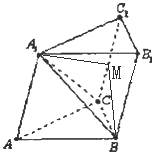
【题目】斜三棱柱ABC﹣A1B1C1中,AA1=AC=BC=2,∠A1AC=∠C1CB=60°,且平面ACC1A1⊥平面BCC1B1 , 则A1B的长度为 . 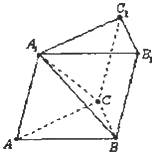
【答案】![]()
【解析】取CC1中点M连接A1M与BM,
∵斜三棱柱ABC﹣A1B1C1中,AA1=AC=BC=2,∠A1AC=∠C1CB=60°,
∴三角形A1CC1是等边三角形,四边形ACC1A1≌四边形BCC1B1
∴A1M⊥CC1 ,
∴BM⊥CC1 ,
∴A1M=BM= ![]()
又平面ACC1A1⊥平面BCC1B1 ,
∴角A1MB是二面角的平面角,故其是直角
∴在直角三角形A1MB由勾股定理可算得
A1B= ![]()
故应填 ![]()
【考点精析】本题主要考查了平面与平面垂直的性质的相关知识点,需要掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直才能正确解答此题.

练习册系列答案
相关题目
【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由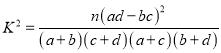 算得
算得![]() .
.
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”
C. 有![]() 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”
D. 有