题目内容
19.如果椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1弦被点A(1,1)平分,那么这条弦所在的直线方程是x+4y-5=0.分析 设这条弦与椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1交于P(x1,y1),Q(x2,y2),由中点坐标公式和P,Q坐标代入椭圆方程,由作差,即可求得直线PQ的斜率,由点斜式方程,即可得到所求直线方程.
解答 解:设这条弦与椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1交于P(x1,y1),Q(x2,y2),
由中点坐标公式知x1+x2=2,y1+y2=2,
把P(x1,y1),Q(x2,y2)代入x2+4y2=36,
得$\left\{\begin{array}{l}{{{x}_{1}}^{2}+4{{y}_{1}}^{2}=36①}\\{{{x}_{2}}^{2}+4{{y}_{2}}^{2}=36②}\end{array}\right.$,
①-②,得2(x1-x2)+8(y1-y2)=0,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{4}$,
∴这条弦所在的直线的方程y-1=-$\frac{1}{4}$(x-1),
即为x+4y-5=0,
由(1,1)在椭圆内,则所求直线方程为x+4y-5=0.
故答案为:x+4y-5=0.
点评 本题考查椭圆的方程的运用,运用点差法和中点坐标和直线的斜率公式是解题的关键.

练习册系列答案
相关题目
7.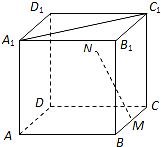 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
9.椭圆ax2+by2=1与直线y=1-x交于A、B两点,过原点与线段AB中点的直线的斜率为$\frac{\sqrt{3}}{2}$,则$\frac{b}{a}$值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{27}$ |