题目内容
12.已知正项数列{an}的前n项和为Sn,数列{bn}的前n项和为Tn,且8Sn=(an+2)2,bn=$\frac{1}{2}$anλn-1(λ>0,λ∈R).(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn;
(3)若不等式(1-λ)Tn+λbn≥2λn对任意的n∈N*恒成立,求λ的取值范围.
分析 (1)通过an+1=Sn+1-Sn计算即得结论;
(2)通过an=4n-2可知bn=(2n-1)λn-1,利用错位相减法计算可知(1-λ)Tn=1+2λ+2λ2+…+2λn-1-(2n-1)λn,分λ=1、λ≠1两种情况讨论即可;
(3)易知当λ=1时不满足题意;当λ≠1时化简得$\frac{1+λ}{1-λ}$≥$\frac{4-2λ}{1-λ}$•λn,分0<λ<1、λ≥2、1<λ<2三种情况讨论即可.
解答 解:(1)由题意,得Sn=$\frac{1}{8}$(an+2)2,
当n=1时,a1=$\frac{1}{8}$$({a}_{1}+2)^{2}$,得a1=2;
当n≥2时,Sn+1=$\frac{1}{8}$$({a}_{n+1}+2)^{2}$.
∴an+1=Sn+1-Sn=$\frac{1}{8}$[$({a}_{n+1}+2)^{2}$-(an+2)2],
整理,得:(an+1+an)(an+1-an-4)=0.
由题意知an+1+an≠0,
所以an+1-an=4,
所以数列{an}为首项为2、公差为4的等差数列,即an=4n-2;
(2)∵an=4n-2,
∴bn=$\frac{1}{2}$(4n-2)λn-1=(2n-1)λn-1,
Tn=1+3λ+5λ2+…+(2n-1)λn-1,
λTn=λ+3λ2+…+(2n-3)λn-1+(2n-1)λn,
两式相减得:(1-λ)Tn=1+2λ+2λ2+…+2λn-1-(2n-1)λn,
①当λ=1时,Tn=1+3+5+…+(2n-1)=n2;
②当λ≠1时,(1-λ)Tn=1+$\frac{2λ(1-{λ}^{n-1})}{1-λ}$-(2n-1)λn,
∴Tn=$\frac{1}{1-λ}$+$\frac{2λ(1-{λ}^{n-1})}{(1-λ)^{2}}$-$\frac{(2n-1){λ}^{n}}{1-λ}$;
综上所述:Tn=$\left\{\begin{array}{l}{\frac{1}{1-λ}+\frac{2λ(1-{λ}^{n-1})}{(1-λ)^{2}}-\frac{(2n-1){λ}^{n}}{1-λ}(λ≠1)}\\{{n}^{2}(λ=1)}\end{array}\right.$;
(3)当λ=1时,Tn=1+3+5+…+(2n-1)=n2,
(1-λ)Tn+λbn=2n-1≥2不成立;
当λ≠1时,(1-λ)Tn=1+$\frac{2λ(1-{λ}^{n-1})}{1-λ}$-(2n-1)λn,
∴(1-λ)Tn+λbn=$\frac{1+λ}{1-λ}$-$\frac{2{λ}^{n}}{1-λ}$,
由题意得:$\frac{1+λ}{1-λ}$-$\frac{2{λ}^{n}}{1-λ}$≥2λn,
$\frac{1+λ}{1-λ}$≥$\frac{4-2λ}{1-λ}$•λn,
①当0<λ<1时,要$\frac{1+λ}{4-2λ}$≥λn对任意n∈N*恒成立.
只要有$\frac{1+λ}{4-2λ}$≥λ即可,解得λ≤$\frac{1}{2}$或λ≥1.
因此,当0<λ≤$\frac{1}{2}$时,结论成立.
②当λ≥2时,$\frac{1+λ}{1-λ}$≥$\frac{4-2λ}{1-λ}$•λn显然不可能对任意n∈N*恒成立.
③当1<λ<2时,只要$\frac{1+λ}{4-2λ}$≤λn对任意n∈N*恒成立.
只要有$\frac{1+λ}{4-2λ}$≤λ即可,解得$\frac{1}{2}$≤λ≤1.
因此当1<λ<2时,结论不成立.
综上可知,实数λ的取值范围为(0,$\frac{1}{2}$].
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 假设三个连续正整数a,b,c都不能被2整除 | |
| B. | 假设三个连续正整数a,b,c都能被2整除 | |
| C. | 假设三个连续正整数a,b,c至多有一个能被2整除 | |
| D. | 假设三个连续正整数a,b,c至多有两个能被2整除 |
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
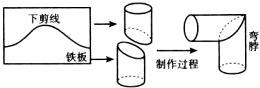 铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.
铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.